Potencial eléctrico debido a una superficie esférica
De Laplace
Contenido |
1 Enunciado
Halle el potencial eléctrico en todos los puntos del espacio creado por una carga Q distribuida uniformemente sobre una superficie esférica de radio R.
2 Introducción
El potencial debido a esta distribución de carga puede hallarse a partir del campo eléctrico que produce. Éste puede hallarse aplicando la ley de Gauss, con el resultado
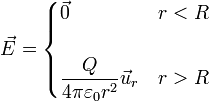
siendo r la distancia al centro de la esfera y 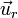 el unitario en la dirección radial y sentido hacia el exterior.
el unitario en la dirección radial y sentido hacia el exterior.
En palabras este resultado nos dice que el campo eléctrico creado por una superficie esférica uniformemente cargada es nulo en su interior y en el exterior es equivalente al de una carga puntual situada en el centro de la esfera.
Para hallar el potencial eléctrico debemos asignar en primer lugar un punto de referencia (la “tierra”) para el cual el potencial es cero. En este caso, lo más sencillo es elegir el infinito como origen de potencial
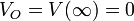
Para cualquier otro punto, su potencial eléctrico se halla integrando el campo eléctrico a lo largo de un camino que va desde el origen de potencial hasta el punto en cuestión
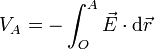
Como camino de integración puede elegirse uno arbitrario.
Teniendo en cuenta la expresión del campo eléctrico, tenemos dos casos: puntos del interior de la esfera y puntos exteriores a ella.
3 En un punto del exterior
Puesto que el campo eléctrico es radial, el camino de integración más sencillo es una semirrecta que va desde el infinito hasta el punto donde queremos hallar el potencial.
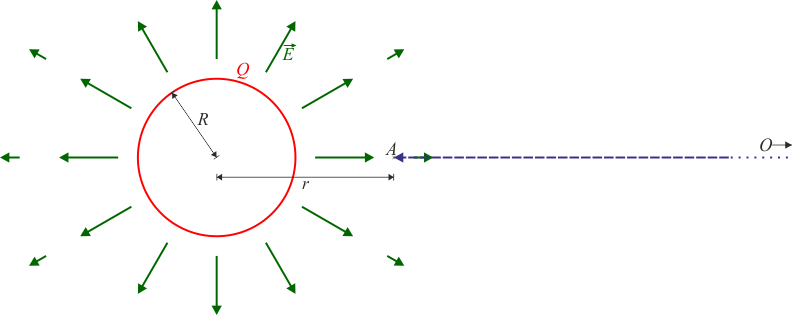
En ese caso
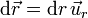
y la integral se reduce a
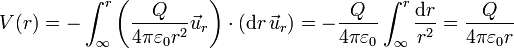
Es decir, obtenemos que el potencial en el exterior equivale al de una carga puntual situada en el centro de la esfera. Esto es completamente lógico, ya que si el campo en todos los puntos exteriores es como el de una carga puntual, su integral también lo es.
4 En un punto del interior
A la hora de hallar el potencial en el interior, existe la tentación de decir “puesto que el campo es cero, el potencial es cero”, pero esto no es correcto. De que el campo eléctrico sea nulo solo se deduce que su integral, el potencial, es una constante. Tenemos que hallar el valor de esta constante.
Como en el caso exterior, hallamos el potencial eléctrico integrando desde el origen de potencial
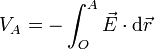
En esta integral el integrando no es nulo. El campo se anula en el interior de la esfera, pero la integral se calcula viniendo desde el infinito, por lo que contiene un tramo exterior.
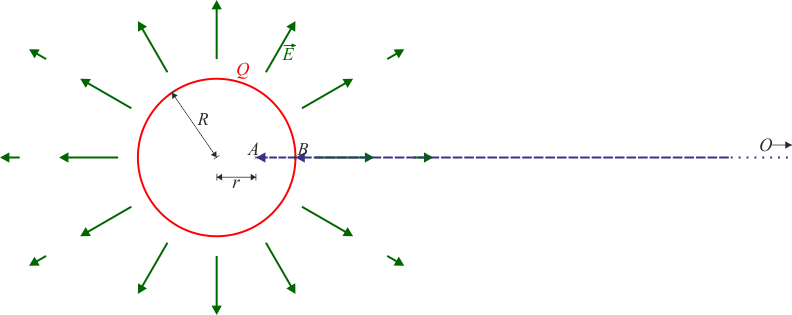
Considerando un camino rectilíneo, dividimos la integral en dos partes, una hasta el punto B en que toca a la esfera y otra desde ahí hasta A
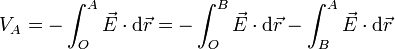
Sustituyendo la expresión del campo en cada región queda
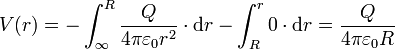
Efectivamente resulta una constante (es independiente de la posición del punto A) igual al potencial eléctrico en la superficie de la esfera.
5 Resumen
Reuniendo los dos resultados obtenemos la expresión para el potencial
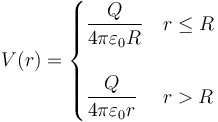
Puesto que el potencial es una función continua, para el caso r = R se puede usar cualquiera de las dos expresiones.






