No Boletín - Otro movimiento de partícula sujeta de un hilo (Ex.Sep/12)
De Laplace
Contenido |
1 Enunciado
La barra rígida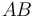 
, de longitud 
, se halla contenida en el plano vertical 
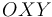y rota alrededor de su extremo fijo 
, cuya posición viene dada por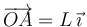 
. Un hilo inextensible, de longitud 
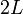, tiene uno de sus extremos conectado a un deslizador puntual 
que puede desplazarse sobre el eje vertical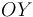 
, mientras que del otro extremo cuelga una partícula 
que mantiene al hilo tenso.
El hilo se apoya sobre una pequeña polea de radio despreciable situada en el extremo B de la barra, y el movimiento del mecanismo es tal que el tramo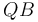 
permanece siempre paralelo al eje 
, y el tramo 
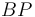permanece siempre paralelo al eje 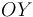(ver figura).
- Determine el vector de posición de la partícula en función del ángulo que forma la barra 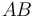con el eje , es decir,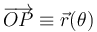
.
- Para la ley horaria
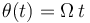(donde 
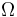es una constante positiva conocida, y 
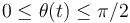), halle los vectores velocidad y aceleración de la partícula P en función del tiempo.
- Sólo para el instante en que
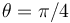, determine las componentes intrínsecas de la aceleración y el radio de curvatura de la partícula P.
2 Vector de posición
El vector de posición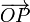 
se puede descomponer en la suma vectorial:
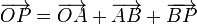
siendo
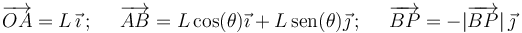
El módulo de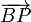 
se calcula a partir de la longitud del hilo 
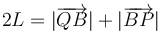, resultando:
![|\overrightarrow{BP}| = 2L-|\overrightarrow{QB}|=2L-[L+L\cos(\theta)]=L-L\cos(\theta)](/wiki/images/math/b/f/c/bfc2047f40be7640ce0417ef3a2363ad.png)
Sustituyendo:
![\overrightarrow{OP} = L\left[1+\cos(\theta)\right]\vec{\imath}+L\left[\mathrm{sen}(\theta)+\cos(\theta)-1\right]\vec{\jmath}](/wiki/images/math/b/a/3/ba3f8cd11faf82d1ef90b17ab8c1cddd.png)
3 Vectores velocidad y aceleración para la ley horaria θ(t) = Ωt
Se sustituye la ley horaria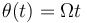 
en la expresión del vector de posición obtenida en el apartado anterior:
![\overrightarrow{OP} = L\left[1+\cos(\Omega t)\right]\vec{\imath}+L\left[\mathrm{sen}(\Omega t)+\cos(\Omega t)-1\right]\vec{\jmath}](/wiki/images/math/e/0/f/e0f7b846c2431a1cae7d40810baa0878.png)
Derivando el vector de posición respecto al tiempo y teniendo en cuenta que Ω es una constante conocida, se obtiene el vector 
en función del tiempo:
![\vec{v}(t) = -\Omega L\,\mathrm{sen}(\Omega t)\,\vec{\imath}+\Omega L\left[\cos(\Omega t)-\mathrm{sen}(\Omega t)\right]\vec{\jmath}](/wiki/images/math/7/f/6/7f64417c34ccd7c46feaf0dc880a0a50.png)
Y derivando el vector velocidad respecto al tiempo, se obtiene el vector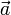 
en función del tiempo:
![\vec{a}(t) = -\Omega^2 L\cos(\Omega t)\,\vec{\imath}-\Omega^2 L\left[\mathrm{sen}(\Omega t)+\cos(\Omega t)\right]\vec{\jmath}](/wiki/images/math/a/0/0/a00e70b239eb8dde257b61622d3b986e.png)
4 Componentes intrínsecas de la aceleración y radio de curvatura cuando θ = π / 4
Evaluemos en primer lugar los vectores velocidad y aceleración para el instante en que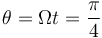 
, es decir, para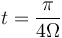 
![t=\displaystyle\frac{\pi}{4\Omega}\,\,\longrightarrow\,\,\left\{\begin{array}{l} \vec{v}=-\Omega L\,\mathrm{sen}\left(\displaystyle\frac{\pi}{4}\right)\,\vec{\imath}+\Omega L\left[\mathrm{cos}\left(\displaystyle\frac{\pi}{4}\right)-\mathrm{sen}\left(\displaystyle\frac{\pi}{4}\right)\right]\vec{\jmath}=-\displaystyle\frac{\sqrt{2}\,\Omega L}{2}\,\vec{\imath} \\ \\ \vec{a}=-\Omega^2 L\,\mathrm{cos}\left(\displaystyle\frac{\pi}{4}\right)\,\vec{\imath}-\Omega^2 L\left[\mathrm{sen}\left(\displaystyle\frac{\pi}{4}\right)+\mathrm{cos}\left(\displaystyle\frac{\pi}{4}\right)\right]\vec{\jmath}=-\displaystyle\frac{\sqrt{2}\,\Omega^2 L}{2}\,\vec{\imath}-\sqrt{2}\,\Omega^2 L\,\vec{\jmath} \end{array}\right.](/wiki/images/math/f/e/e/fee81d1d71e1090ec3bbc0cc38bc4086.png)
Las componentes intrínsecas de la aceleración y el radio de curvatura en el citado instante de tiempo se pueden obtener a partir de las siguientes expresiones:
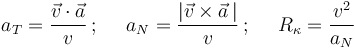
Operando:
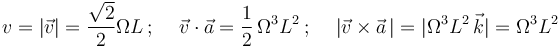
Y sustituyendo en las expresiones anteriores, se obtiene:
