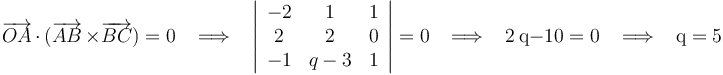No Boletín - La coplanariedad de tres vectores (Ex.Oct/13)

De Laplace

(Redirigido desde No Boletín - Coplanariedad de tres vectores (Ex.Oct/13))

1 Enunciado

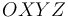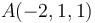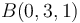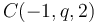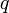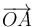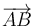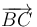En un triedro cartesiano $OXYZ\,$ se consideran los puntos $A(-2,1,1)\,$ , $B(0,3,1)\,$ y $C(-1,q,2)\,$ . ¿Cuál es el valor de $q\,$ si los vectores $\overrightarrow{OA}\,$ , $\overrightarrow{AB}\,$ y $\overrightarrow{BC}\,$ son coplanarios?

2 Solución

Las coordenadas de un punto en un sistema de ejes cartesianos son las componentes de su vector de posición en la base ortonormal asociada, es decir:

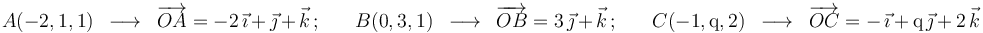
$A(-2,1,1)\,\,\,\longrightarrow\,\,\,\overrightarrow{OA}=-2\,\vec{\imath}\,+\,\vec{\jmath}\,+\,\vec{k}\,;\,\,\,\,\,\,\,\,\,\, B(0,3,1)\,\,\,\longrightarrow\,\,\,\overrightarrow{OB}=3\,\vec{\jmath}\,+\,\vec{k}\,;\,\,\,\,\,\,\,\,\,\, C(-1,\mathrm{q},2)\,\,\,\longrightarrow\,\,\,\overrightarrow{OC}=-\,\vec{\imath}\,+\,\mathrm{q}\,\vec{\jmath}\,+\,2\,\vec{k}$

Y, por otra parte:

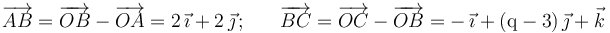
$\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=2\,\vec{\imath}+2\,\vec{\jmath}\,;\,\,\,\,\,\,\,\,\,\, \overrightarrow{BC}=\overrightarrow{OC}-\overrightarrow{OB}=-\,\vec{\imath}+(\mathrm{q}-3)\,\vec{\jmath}+\vec{k}$

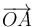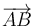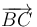Exigiendo la condición de coplanariedad (producto mixto nulo) a los vectores $\overrightarrow{OA}\,$ , $\overrightarrow{AB}\,$ y $\overrightarrow{BC}\,$ , deducimos el valor de q:

$\overrightarrow{OA}\,\cdot\,(\overrightarrow{AB}\,\times\overrightarrow{BC})=0\,\,\,\,\,\Longrightarrow\,\,\,\,\,\left|\begin{array}{ccc} -2 & 1 & 1 \\ 2 & 2 & 0 \\ -1 & q-3 &1 \end{array}\right|=0\,\,\,\,\,\Longrightarrow\,\,\,\,\,2\,\mathrm{q}-10=0\,\,\,\,\,\Longrightarrow\,\,\,\,\,\mathrm{q}=5$

No Boletín - La coplanariedad de tres vectores (Ex.Oct/13)

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES