No Boletín - Fuerza, momento cinético y trabajo (Ex.Ene/12)
De Laplace
Contenido |
1 Enunciado
Una partícula P, de masa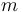 
y no vinculada, se mueve con respecto a un sistema de referencia OXYZ conforme a la ecuación horaria:
![\overrightarrow{OP}\equiv\vec{r}(t)=b\,[\mathrm{cos}(\omega t)\,\vec{\imath}+\sqrt{2}\,\mathrm{sen}(\omega t)\,\vec{\jmath}\,\,]](/wiki/images/math/8/c/d/8cdf92d42a59817fed618f8f45d78a59.png)
donde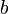 
y 
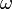son constantes conocidas.
- ¿Qué fuerza neta
actúa sobre la partícula?
- ¿Cuánto vale el momento cinético de la partícula respecto al origen de coordenadas?
- ¿Cuál es el valor del trabajo neto realizado sobre la partícula entre
y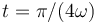 
?
2 Fuerza neta
Derivando el vector de posición de la partícula P respecto al tiempo una y dos veces, obtenemos su velocidad y su aceleración, respectivamente:
![\vec{v}=\displaystyle\frac{d\vec{r}}{dt}=\omega b\,[-\mathrm{sen}(\omega t)\,\vec{\imath}+\sqrt{2}\,\mathrm{cos}(\omega t)\,\vec{\jmath}\,\,]
\,;\,\,\,\,\,\,\,\,\,
\vec{a}=\displaystyle\frac{d\vec{v}}{dt}=-\omega^2 b\,[\mathrm{cos}(\omega t)\,\vec{\imath}+\sqrt{2}\,\mathrm{sen}(\omega t)\,\vec{\jmath}\,\,]=-\omega^2\vec{r}](/wiki/images/math/0/5/2/052f40654b622f122b41e85db26b0932.png)
Y conforme a la segunda ley de Newton, la fuerza neta que actúa sobre la partícula P es:
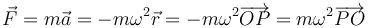
Observamos que la recta de acción de la fuerza neta sobre P pasa en todo instante por el origen de coordenadas O. Se trata, pues, de un movimiento bajo fuerza central (con centro en O).
3 Momento cinético
El momento cinético de la partícula P respecto al origen de coordenadas O se calcula a partir de su definición:
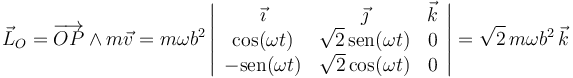
Al tratarse de un movimiento bajo fuerza central (con centro en O), se obtiene que el momento cinético (respecto a O) es constante a lo largo del tiempo (es una integral primera del movimiento).
4 Trabajo
Calculamos el trabajo que nos piden mediante el teorema de las fuerzas vivas:
![W_{0}^{\pi/4\,\omega}=K\left(\frac{\pi}{4\,\omega}\right)-K(0)=\frac{1}{2}m\,\left[v^2\left(\displaystyle\frac{\pi}{4\,\omega}\right)-v^2(0)\right]=\frac{1}{2}m\omega^2b^2\left[\mathrm{sen}^2\left(\frac{\pi}{4}\right)+2\,\mathrm{cos}^2\left(\frac{\pi}{4}\right)-\mathrm{sen}^2\left(0\right)-2\,\mathrm{cos}^2\left(0\right)\right]=-\frac{1}{4}m\omega^2b^2](/wiki/images/math/4/2/c/42cfa19631a659bda9b1c140cb6442b1.png)
