Equilibrio de una partícula sobre una esfera lisa (GIA)
De Laplace
Contenido |
1 Enunciado
Un punto material M de peso P está obligado a permanecer en la superficie de una esfera de radio R y centro O. Además, M es atraído por un punto fijo A del ecuador de la superficie esférica, debido a la existencia de un resorte elástico ideal, de longitud natural nula y de constante recuperadora 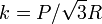 , que conecta ambos puntos. Determina las posiciones de equilibrio del punto material M, y la fuerza de reacción vincular en ellas.
, que conecta ambos puntos. Determina las posiciones de equilibrio del punto material M, y la fuerza de reacción vincular en ellas.
2 Solución
2.1 Ecuaciones de equilibrio
Se trata de determinar la posición de equilibrio de un punto material que está obligado a moverse en una superficie dada. Para una partícula libre, el vector que indica su posición en el espacio se escribe, en general,
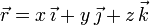
En este caso, la superficie impone una ligadura bilateral: la ecuación que cumplen los puntos situados sobre una superficie esférica de radio R

La condición de equilibrio mecánico para un punto material es que la
suma de fuerzas sobre él sea nula. Aquí tenemos tres fuerzas,
el peso  , la fuerza ejercida por el muelle,
, la fuerza ejercida por el muelle, 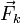 y la
fuerza de reacción vincular que impide que el punto penetre en la
esfera,
y la
fuerza de reacción vincular que impide que el punto penetre en la
esfera,  . Veamos la expresión de cada una de ellas.
. Veamos la expresión de cada una de ellas.
El peso apunta en la dirección negativa del eje OZ que hemos elegido, es decir

La fuerza 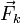 es proporcional a la distancia entre el punto y el
punto de sujeción del muelle, pues el enunciado dice que su longitud
natural es cero. La posición de este punto es
es proporcional a la distancia entre el punto y el
punto de sujeción del muelle, pues el enunciado dice que su longitud
natural es cero. La posición de este punto es 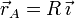 . Por
tanto
. Por
tanto

Recordemos que z viene dada en función de x e y a través de la ecuación de la esfera.
Por ultimo la fuerza de reacción vincular  es normal a
la superficie, pues suponemos que el contacto es liso. Tenemos
es normal a
la superficie, pues suponemos que el contacto es liso. Tenemos
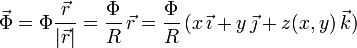
Hemos usado que en cada punto de la esfera podemos construir un vector
unitario perpendicular a ella dividiendo el vector de posición de ese
punto por su módulo, 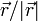 . Y para todos los puntos en la
superficie
. Y para todos los puntos en la
superficie 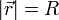 . Para resolver el problema vamos a suponer que el vínculo es no rugoso y que la
partícula se mueve sobre la superficie de la esfera. Por tanto, la f.r.v. sólo puede estar
dirigida hacia el exterior de la superficie. Si estuviera dirigida hacia dentro querría decir que habría
una fuerza adhesiva entre la superficie y la partícula, con lo que el vinculo no sería liso.
. Para resolver el problema vamos a suponer que el vínculo es no rugoso y que la
partícula se mueve sobre la superficie de la esfera. Por tanto, la f.r.v. sólo puede estar
dirigida hacia el exterior de la superficie. Si estuviera dirigida hacia dentro querría decir que habría
una fuerza adhesiva entre la superficie y la partícula, con lo que el vinculo no sería liso.
Ahora podemos plantear la condición de equilibrio para el punto
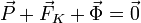
Igualando a cero las componentes de esta ecuación vectorial obtenemos tres ecuaciones escalares, a las que añadimos la ecuación que deben cumplir las coordenadas de los puntos sobre una esfera de radio R
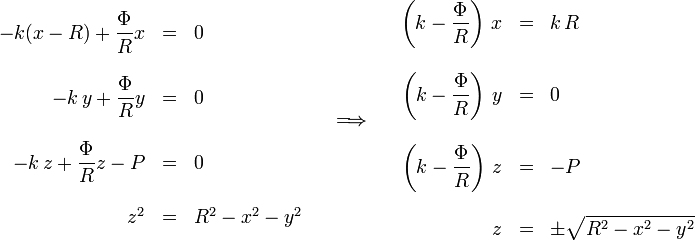
2.2 Análisis de las soluciones
Las incógnitas del problema son Φ, x, y y z. En la segunda ecuación
(k − Φ / R) no puede ser cero, pues entonces, de la primera ecuación
tendríamos 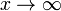 . Así pues
. Así pues
Dividiendo la primera ecuación por la tercera y teniendo en cuenta la ecuación de la esfera obtenemos
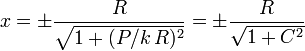
siendo el parámetro C
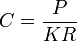
Este parámetro mide la importancia relativa del peso y la fuerza ejercida por el muelle. Si 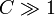 la fuerza del
muelle es despreciable frente a la del peso. Si
la fuerza del
muelle es despreciable frente a la del peso. Si 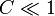 es el peso el que es despreciable frente a la fuerza del
muelle.
es el peso el que es despreciable frente a la fuerza del
muelle.
Para cada valor de x tenemos dos posibles valores de z (recordemos que y = 0)
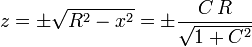
Es decir, hay cuatro posibles puntos de equilibrio.
A su vez, la componente de la fuerza de reacción vincular puede despejarse de la primera y de la tercera ecuación de equilibrio. Obtenemos entonces dos posibles valores de Φ para cada par de valores de x y z. Para que el punto sea solución de equilibrio estos dos valores deben coincidir. Resumimos las posibilidades en la siguiente tabla
| Punto | x | z | Φ de x | Φ de z | Posible |
|---|---|---|---|---|---|
| P1 | 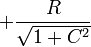 | 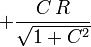
| 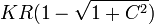 | 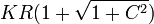
| NO |
| P2 | 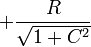 | 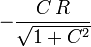
| 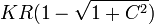 | 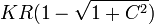
| SÍ |
| P3 | 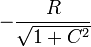 | 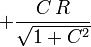
| 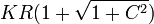 | 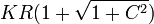
| SÍ |
| P4 | 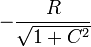 | 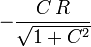
| 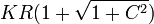 | 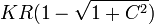
| NO |
Sólo los puntos P2 y P3 dan el mismo valor de Φ al despejarla de la primera y tercera ecuaciones de equilibrio.
En el caso del punto P2, como el parámetro C es siempre positivo tenemos
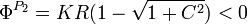
Este signo significa que la fuerza de reacción vincular apuntaría hacia el centro de la esfera. Pero si el vínculo es liso esto no es posible. La partícula esta sobre la superficie de la esfera, no pegada a ella. Una fuerza hacia dentro supondría que hay algún tipo de pegamento entre la partícula y la esfera. Por tanto, esta solución no es posible.
Así pues, el único punto de equilibrio es el P3. Las coordenadas y la componente de la fuerza de reacción vincular son
| x | y | z | Φ |
|---|---|---|---|
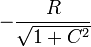 | 0 | 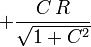
| 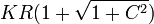
|
con C = P / KR.
Puede verse gráficamente que el único punto posible de equilibrio es el P3. La figura muestra
la dirección de las fuerzas en cada uno de los puntos de equilibrio, teniendo en cuenta que la fuerza de reacción
vincular sólo puede apuntar hacia el exterior de las esferas. El único punto en el que la suma vectorial de
las tres fuerzas puede dar cero es en el P3. En el P1 y el P4, si proyectamos
las fuerzas en las direcciones paralela y perpendicular a  , vemos que siempre queda una
componente no nula perpendicular a
, vemos que siempre queda una
componente no nula perpendicular a  . Lo mismo ocurre en P2 si proyectamos en las direcciones
paralela y perpendicular a
. Lo mismo ocurre en P2 si proyectamos en las direcciones
paralela y perpendicular a 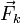 .
.
2.3 Caso límite cuando el muelle es muy fuerte
Vamos a considerar la situación en que se cumple
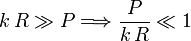
Esto ocurre si la constante del muelle es muy grande, es decir, cuando tenemos un muelle muy fuerte. Para obtener el valor aproximado usaremos el desarrollo de Taylor

En las soluciones para x y Φ consideramos 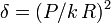 ,
con lo cual los valores aproximados de x y Φ en este caso límite
,
con lo cual los valores aproximados de x y Φ en este caso límite

Es decir, si el muelle tira muy fuerte la posición de equilibrio de la masa es el punto opuesto de la esfera respecto al punto de sujeción del muelle, y la fuerza de reacción vincular depende responde sólo a la fuerza del muelle, pues entonces la contribución del peso es despreciable.







