Derivada en una dimensión
De Laplace
Contenido |
1 Definición
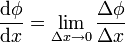
Gráficamente, antes de tomar el límite, el cociente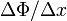 
representa la pendiente de una recta secante a la gráfica de la función, siendo uno de los puntos de corte aquél en que queremos calcular la derivada y el otro que vamos acercando progresivamente hacia el primer punto. Cuando tomamos el límite, ambos puntos coinciden y la secante se convierte en la tangente.
Podemos interpretar la expresión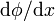 
de dos formas.
2 La derivada como cociente
La definición como límite de un cociente permite leer la expresión 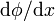como un cociente en sí mismo, entre:
- La cantidad
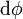, conocida como el diferencial de la función 
. Este diferencial se interpreta como un incremento infinitamente pequeño de la función entre dos puntos vecinos.
- La cantidad dx,, conocida como el diferencial de
, que representa la diferencia entre dos posiciones infinitamente próximas.
De esta interpretación como cociente se obtiene de forma inmediata que, por ejemplo, las dimensiones de la derivada 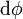son las de divididas por las de (verbigracia, que si el espacio se mide en metros y el tiempo en segundos, la velocidad -que es la derivada del espacio respecto al tiempo- se mide en metros/segundo).
La interpretación de la derivada como cociente no se extiende a las derivadas de orden superior. La segunda derivada
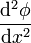
no se puede entender como el cociente d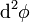e 
entre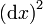 
, a menos que definamos de una forma muy precisa qué significa 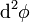. En cualquier caso, no es un cociente ordinario y, sobre todo,
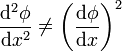
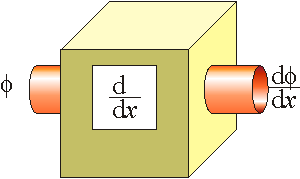
3 La derivada como operador
podemos leerlos como algo que se "multiplica" por . Ese algo no es un número ni una función sino un operador.
Podemos imaginar un operador como una máquina con una entrada y una salida. Por la entrada se introduce la función y por la salida se obtiene su derivada.
Los operadores se pueden componer, de forma que al resultado de la aplicación de un operador se le puede aplicar otro o él mismo. Así, la segunda derivada equivale a la aplicación reiterada del operador derivada
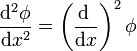
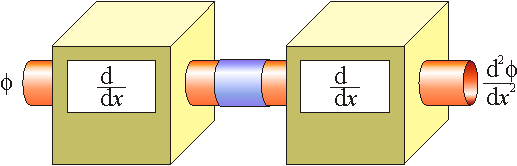
Por la forma de actuar, la aplicación de un operador tiene elementos en común con la multiplicación ordinaria, pero no es una multiplicación. El operador en si mismo no es nada, solo su resultado es una magnitud física.
