No Boletín - Cuestión sobre EIRMD (Ex.Ene/12)

De Laplace

(Redirigido desde Cuestión sobre EIRMD (Ex.Ene/12))

1 Enunciado

Dos puntos de un sólido rígido con movimiento helicoidal instantáneo (MHI) tienen las siguientes posiciones y velocidades:

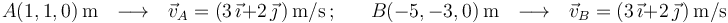
$A(1,1,0)\,\mathrm{m}\,\,\,\,\longrightarrow\,\,\,\,\vec{v}_A=(3\,\vec{\imath}+2\,\vec{\jmath}\,)\,\mathrm{m/s}\,; \,\,\,\,\,\,\,\,\,\, B(-5,-3,0)\,\mathrm{m}\,\,\,\,\longrightarrow\,\,\,\, \vec{v}_B=(3\,\vec{\imath}+2\,\vec{\jmath}\,)\,\mathrm{m/s}$

¿Dónde se halla el eje instantáneo de rotación y mínimo deslizamiento (EIRMD)?

2 Solución

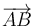Por tratarse de un MHI, sabemos que el campo de velocidades no es uniforme (la velocidad angular es no nula). Por tanto, el hecho observado de que las velocidades de los puntos $A\,$ y $B\,$ sean iguales implica que el vector velocidad angular es paralelo al vector $\overrightarrow{AB}\,$ :

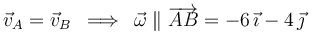
$\vec{v}_A=\vec{v}_B\,\,\,\Longrightarrow\,\,\,\vec{\omega}\parallel\overrightarrow{AB}=-6\,\vec{\imath}-4\,\vec{\jmath}$

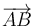Pero es inmediato comprobar que las propias velocidades de los puntos $A\,$ y $B\,$ también son paralelas a dicho vector $\overrightarrow{AB}\,$ . Por tanto, los puntos $A\,$ y $B\,$ pertenecen al EIRMD (porque sus velocidades son paralelas al vector velocidad angular):

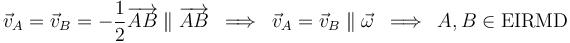
$\vec{v}_A=\vec{v}_B=-\frac{1}{2}\overrightarrow{AB}\parallel\overrightarrow{AB}\,\,\,\Longrightarrow\,\,\,\vec{v}_A=\vec{v}_B\parallel\vec{\omega}\,\,\,\Longrightarrow\,\,\,A,B\in \mathrm{EIRMD}$

Podemos concluir que el EIRMD es la recta que pasa por los puntos $A\,$ y $B\,$ .

No Boletín - Cuestión sobre EIRMD (Ex.Ene/12)

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES