No Boletín - Composición de dos rotaciones concurrentes (Ex.Dic/11)
De Laplace
1 Enunciado
Se tienen tres sólidos tales que el movimiento relativo {20} es una rotación en torno al eje {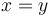 ,
, 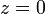 } y el movimiento de arrastre {01} es una rotación en torno al eje {
} y el movimiento de arrastre {01} es una rotación en torno al eje { ,
, 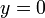 }. Las velocidades angulares de ambos movimientos tienen el mismo módulo
}. Las velocidades angulares de ambos movimientos tienen el mismo módulo 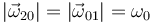 y sus respectivas componentes-
y sus respectivas componentes-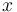 son ambas positivas.
son ambas positivas.
- ¿Qué tipo de movimiento es el absoluto {21}?
- ¿Cuál es el EIR (o EIRMD) de dicho movimiento {21}?
2 Solución
La dirección del vector 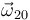 es la dirección del EIR{20} dado. Como también se nos dice el módulo (
es la dirección del EIR{20} dado. Como también se nos dice el módulo (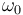 ) y el sentido (componente-
) y el sentido (componente-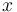 positiva) de dicho vector, estamos en condiciones de escribir su valor:
positiva) de dicho vector, estamos en condiciones de escribir su valor:
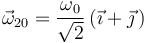
Y como también conocemos la dirección (nos dan el EIR{01}), el módulo (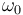 ) y el sentido (componente-
) y el sentido (componente-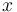 positiva) del vector
positiva) del vector 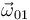 , podemos escribir su valor:
, podemos escribir su valor:
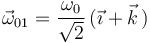
La ley de composición de velocidades angulares nos permite determinar la velocidad angular del movimiento {21}:
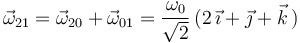
Por otra parte, observando las ecuaciones del EIR{20} y del EIR{01}, nos damos cuenta de que ambos ejes son concurrentes en el origen de coordenadas 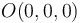 . Por tanto, la velocidad de dicho punto
. Por tanto, la velocidad de dicho punto  es nula en todos los movimientos:
es nula en todos los movimientos:
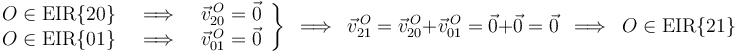
Llegamos, pues, a la conclusión de que el movimiento {21} es una ROTACIÓN PURA, ya que tiene velocidad angular no nula (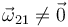 ) y al menos un punto con velocidad nula (
) y al menos un punto con velocidad nula (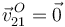 ).
).
El EIR{21} pasa por el origen de coordenadas  (punto con velocidad {21} nula) y su dirección es la dirección del vector velocidad angular del movimiento {21}. Por tanto, las ecuaciones del EIR{21} son:
(punto con velocidad {21} nula) y su dirección es la dirección del vector velocidad angular del movimiento {21}. Por tanto, las ecuaciones del EIR{21} son: