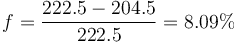Colisión en tiro parabólico
De Laplace
Contenido |
1 Enunciado
En un videojuego que reproduce correctamente las leyes de la física, es preciso golpear una masa de 0.80 kg encajada entre un bloque fijo por abajo y uno idéntico por arriba, de manera que la única forma de sacarlo es mediante un golpe horizontal. Para ello se dispone de un cañón que lanza un proyectil de 0.20kg desde un punto situado a 30m en la horizontal y 20m en la vertical.
- Calcule la velocidad inicial que debe tener el proyectil para impactar el blanco de forma horizontal. ¿Cuánto vale la rapidez inicial? ¿Qué ángulo debe formar la velocidad inicial con el suelo?
- Suponiendo que la colisión es elástica, halle
- Las velocidades del proyectil y el blanco justo tras la colisión
- Las posiciones donde proyectil y blanco impactan con el suelo.
- La proporción de la energía mecánica inicial que tiene el proyectil y la que tiene el blanco en el momento del impacto con el suelo. Tómese este suelo como origen de la energía potencial.
- Suponiendo ahora que la colisión es completamente inelástica, de forma que el proyectil queda empotrado en el blanco, halle:
- La velocidad del conjunto justo tras la colisión
- La posición donde impacta con el suelo.
- La proporción de la energía mecánica inicial que se ha perdido desde el lanzamiento al impacto final.
Tómese g = 10m/s². Desprecie el rozamiento con el aire. Suponga que el proyectil y el blanco son partículas puntuales.
2 Velocidad inicial
En todo lo que sigue, se emplearan las unidades fundamentales del SI (distancias en m, tiempos en s, masas en kg) y productos de ellas.
Por ser un tiro parabólico, el movimiento horizontal es uniforme

y el vertical es uniformemente acelerado

El impacto debe producirse cuando vy = 0, lo que ocurre en
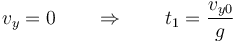
En ese momento la altura debe ser h, la del blanco. Sustituimos t por t1

y por tanto

A este resultado también se llega por conservación de la energía. El valor numérico es
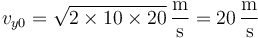
El tiempo que tarda en impactar es
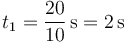
La velocidad horizontal sale de que en el mismo tiempo debe recorrer la distancia horizontal 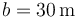
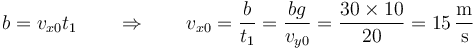
El vector velocidad inicial es entonces
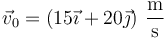
siendo la rapidez inicial
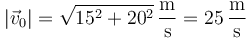
y el ángulo de lanzamiento
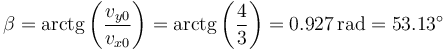
3 Colisión elástica
3.1 Velocidad justo antes del impacto
En el momento que impacta, el proyectil ha perdido su velocidad vertical, pero conserva la horizontal. Justo antes de la colisión, en m/s
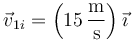
3.2 Velocidad justo tras el impacto
En la colisión se conserva la cantidad de movimiento, por tanto, en el SI
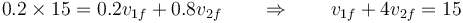
y por ser una colisión elástica, el coeficiente de restitución vale la unidad
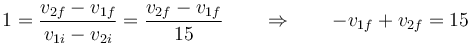
Del sistema de ecuaciones, sumando
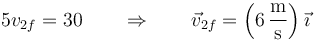
y

3.3 Impactos en el suelo
En su descenso, proyectil y blanco siguen un movimiento uniformemente acelerado, inverso al de la subida y empleando el mismo tiempo, 2 s, en el descenso. Durante ese tiempo el proyectil realiza un desplazamiento

Es negativo porque el proyectil rebota hacia atrás. Teniendo en cuenta los 30m recorridos antes, la posición de impacto es
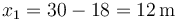
De la misma manera, para el blanco

3.4 Reparto de la energía
En el momento que choca con el suelo, toda su energía es cinética, siendo su velocidad vertical la misma que tenía al iniciar el ascenso (equivale a gt1). Por tanto su energía final es
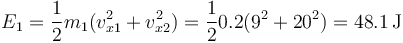
y de la misma manera para el blanco
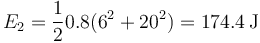
Como en este sistema la energía se conserva, la energía mecánica total final es la misma que la inicial.

Nótese que esta energía inicial incluye tanto la cinética inicial del proyectil como la potencial inicial del blanco, que estaba a 20m de altura.
La proporción que se lleva el proyectil es
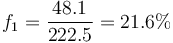
y
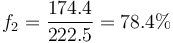
4 Colisión inelástica
Si la colisión es completamente inelástica, el proyectil se fusiona con el blanco y la velocidad tras la colisión es la misma para los dos (C=0). En ese caso, por conservación de la cantidad de movimiento

El punto de impacto es ahora
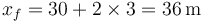
siendo la energía final
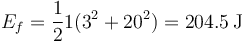
Puesto que la energía inicial es la misma que antes, 222.5J, la proporción de la energía que se pierde es