Cuestión de Cinemática del Punto, F1 GIA (Sept, 2012)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

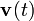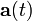Una partícula se mueve con velocidad y aceleración instantáneas, $\mathbf{v}(t)$ y $\mathbf{a}(t)$ , tales que su producto escalar tiene un valor $k 2$ , constante en el tiempo, y su producto vectorial es un vector 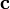$\mathbf{c}$ , también constante. Considerando que en el instante inicial el móvil se desplaza con una celeridad de valor conocido $v 0$ , determine las siguientes magnitudes:

Ángulo que forman en cada instante las direcciones de la velocidad y la aceleración.
Ley horaria $v (t)$ que verifica el módulo de la velocidad instantánea (celeridad).
Radio de curvatura de la trayectoria en función de la distancia $s$ recorrida por la partícula, $R κ (s)$ . Suponga que en el instante inicial $s (0) = 0$ .

2 Solución

2.1 Ángulo formado por la velocidad y la aceleración

Como se sabe, el producto escalar de dos vectores definidos en el espacio real, euclídeo y tridimensional es el número real que se obtiene al multiplicar los módulos de aquéllos por el coseno del ángulo que forman sus direcciones y sentidos. Por tanto, en el movimiento bajo estudio, la velocidad y aceleración instantáneas del móvil puntual deben ser tales que, en cualquier instante de tiempo se cumple,

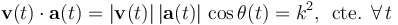
$\mathbf{v}(t)\cdot\mathbf{a}(t)=|\mathbf{v}(t)|\!\ |\mathbf{a}(t)|\!\ \cos\theta(t)=k^2 \mathrm{,}\,\;\,\mathrm{cte.}\;\,\forall\, t$

donde $θ(t)$ es el ángulo que forman las direcciones de dichas magnitudes en un instante arbitrario.

Análogamente, si su producto vectorial de ambos vectores es también un vector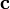 $\mathbf{c}$ de dirección, sentido y módulo constantes en el tiempo, se tendrá que,

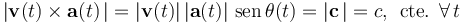
$|\mathbf{v}(t)\times\mathbf{a}(t)\!\ |=|\mathbf{v}(t)|\!\ |\mathbf{a}(t)|\!\ \,\mathrm{sen}\,\theta(t)=|\mathbf{c}\!\ |=c \mathrm{,}\,\;\,\mathrm{cte.}\;\,\forall\, t$

La relación entre el módulo del producto vectorial y el producto escalar de los vectores velocidad y aceleración instantáneas es igual a la tangente del ángulo que en cada instante forman las direcciones de dichas magnitudes. Y como en las condiciones del enunciado esta relación va a tener un valor constante, se tendrá que, dicho ángulo se mantiene invariable durante el movimiento de la partícula:

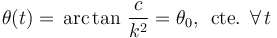
$\frac{|\mathbf{v}(t)\times\mathbf{a}(t)\!\ |}{\mathbf{v}(t)\cdot\mathbf{a}(t)}=\frac{\mathrm{sen}\,\theta(t)}{\cos\theta(t)}=\frac{c}{k^2}\mathrm{,}\,\;\,\mathrm{cte.}\;\,\forall\, t\quad\Longrightarrow$ $\theta(t)=\,\mathrm{arc}\!\ \mathrm{tan}\ \frac{c}{k^2}=\theta_0\mathrm{,}\,\;\,\mathrm{cte.}\;\,\forall\, t$

2.2 Ley horaria para el módulo de la velocidad

Si las longitudes del parámetro de arco “ $s$ ” (es decir, las distancias recorridas por el móvil sobre la trayectoria) se miden en el mismo sentido en que aquél se desplaza, se tendrá que la celeridad, “ $v (t)$ ”, (módulo del vector velocidad), coincide en cada instante con la derivada temporal de la ley horaria $s (t)$ :

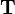$|\mathbf{v}(t)\!\ |=v(t)=\frac{\mathrm{d}s(t)}{\mathrm{d}t}\quad\longrightarrow\quad \mathbf{v}(t)=v(t)\!\ \mathbf{T}$

donde $\mathbf{T}$ es el vector unitario tangente a la trayectoria. Como se sabe, la aceleración instantánea puede descomponerse en una aceleración tangencial colineal con esta dirección, y otra componente en la dirección perpendicular a 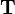$\mathbf{T}$ , denominada aceleración normal:

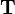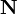$\mathbf{a}(t)=a_\mathrm{T}\!\ \mathbf{T}+a_\mathrm{N}\!\ \mathbf{N}\mathrm{,}\;\quad\mathrm{donde}\;\;\begin{cases}\displaystyle a_\mathrm{T}(t)=\frac{\mathrm{d}v(t)}{\mathrm{d}t}\\ \\ \displaystyle a_\mathrm{N}(t)=\frac{v^2(t)}{R_\kappa}\end{cases}$

Y como $\mathbf{T}$ y $\mathbf{N}$ son vectores unitarios perpendiculares en todos los puntos de la trayectoria del móvil, se tendrá que el el producto escalar de la velocidad y la aceleración instantánea será igual al producto de la celeridad por la componente tangencial de la aceleración. Particularizando este resultado general al caso descrito en el enunciado, obtenemos la ecuación verificada por la celeridad en el movimiento bajo estudio:

$\mathbf{v}(t)\cdot\mathbf{a}(t)=v(t)a_\mathrm{T}(t)=k^2\quad\longrightarrow\quad v(t)\ \frac{\mathrm{d}v(t)}{\mathrm{d}t}=k^2\mathrm{,}\,\;\,\mathrm{cte.}\;\forall\, t$

La solución a esta ecuación diferencial es fácil de obtener, ya que el producto de una función por su derivada es igual a la mitad de la derivada del cuadrado de la función:

$v(t)\ \frac{\mathrm{d}v(t)}{\mathrm{d}t}=k^2\quad\longrightarrow\quad \frac{\mathrm{d}}{\mathrm{d}t}\big[v^2(t)\big]=2\!\ k^2\mathrm{,}\,\;\,\mathrm{cte.}\;\forall\, t\quad\Longrightarrow\quad v^2(t)=2\!\ k^2\!\ t+C$

Obsérvese que la constante de integración $C$ debe ser igual al valor de la celeridad en el instante inicial ( $t = 0$ ), que es un valor conocido $v 0$ ; se tendrá, por tanto:

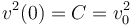
$v^2(0)=C=v_0^2$ $\Rightarrow$ $v(t)=k\!\ \sqrt{2\!\ t+(v_0/k)^2}$

2.3 Radio de curvatura de la trayectoria

Como hemos visto en el apartado anterior, el valor de esta propiedad geométrica en cada punto de la trayectoria seguida por la partícula está directamente relacionada con la componente normal $a N$ de su aceleración. Por otra parte, dicha componente está determinada por el producto vectorial de la velocidad y la aceleración instantáneas:

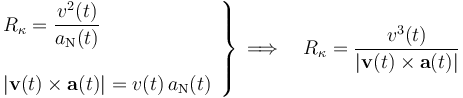
$\left.\begin{array}{l}\displaystyle R_\kappa=\frac{v^2(t)}{a_\mathrm{N}(t)}\\ \\ \displaystyle |\mathbf{v}(t)\times\mathbf{a}(t)|=v(t)\!\ a_\mathrm{N}(t)\end{array}\right\}\,\Longrightarrow\quad R_\kappa=\frac{v^3(t)}{|\mathbf{v}(t)\times\mathbf{a}(t)|}$

Y sustituyendo los datos del enunciado y el resultado anterior, se obtiene una ley que determina el valor del radio de curvatura de la trayectoria en el punto que ocupa el móvil en cada instante:

$R_\kappa(t)=\frac{v^3(t)}{|\mathbf{v}(t)\times\mathbf{a}(t)|}=\frac{k^3}{c}\!\ \big[2\!\ t+(v_0/k)^2\big]^{3/2}$

Sin embargo, resulta mucho más práctico describir las propiedades de la trayectoria independientemente de cómo ésta sea recorrida por un móvil. Para ello, describiremos el radio de curvatura utilizando una propiedad intrínseca de la trayectoria: el parámetro arco “ $s$ ”. Una vez que determinemos la ley horaria correspondiente a dicho parámetro en el movimiento bajo estudio, podemos eliminar la variable tiempo de la expresión de la curvatura sustituyéndola por la distancia recorrida por el móvil desde el instante inicial hasta un instante arbitrario $t$ :

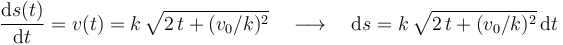
$\frac{\mathrm{d}s(t)}{\mathrm{d}t}=v(t)=k\!\ \sqrt{2\!\ t+(v_0/k)^2}\quad \longrightarrow \quad \mathrm{d}s=k\!\ \sqrt{2\!\ t+(v_0/k)^2}\,\mathrm{d}t$

Integramos teniendo en cuenta la condición inicial $s (0) = 0$ y obtenemos

$s(t)=\frac{1}{3k^2}\left( \big[2k^2 t+v_0^2\big]^{3/2} - v_0^3\right)$ $\Rightarrow$ $R_\kappa(s)=\frac{v_0^3 + 3k^2s}{ c}$

Cuestión de Cinemática del Punto, F1 GIA (Sept, 2012)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Ángulo formado por la velocidad y la aceleración

2.2 Ley horaria para el módulo de la velocidad

2.3 Radio de curvatura de la trayectoria

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES