3.4. Partícula en el interior de un aro
De Laplace
Contenido |
1 Enunciado
Se tiene un aro circular de radio R situado verticalmente. Determine la velocidad que debe comunicarse a una partícula de masa m situada en el punto más bajo del aro para que sea capaz de llegar hasta el punto más alto si la partícula es:
- Una anilla ensartada en el aro
- Una bolita que desliza por el interior del aro, sin estar unida a él.
Calcule la reacción que ejerce el aro sobre la partícula en el punto más bajo y en el más alto, para los dos casos anteriores. Desprecie el rozamiento en todos los casos.
2 Anilla
En el caso de una anilla ensartada en el aro tenemos una partícula que se ve obligada a moverse a lo largo de la circunferencia. Esto constituye un ejemplo de un vínculo bilateral ya que la partícula no puede separarse de la circunferencia ni en un sentido ni en otro.
Podemos obtener la velocidad mínima para que llegue al punto más alto aplicando la ley de conservación de la energía mecánica. Puesto que la fuerza de reacción vincular no realiza trabajo, la única energía potencial es la debida al peso:

La velocidad mínima es aquella que hace llegar a la anilla al punto más alto con velocidad nula. Tomando como origen de energía potencial el punto más bajo del aro, la conservación de la energía nos da
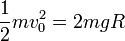
con lo que la velocidad mínima es
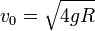
En el punto más alto, la fuerza activa aplicada, el peso, es puramente normal a la trayectoria. La única aceleración de la partícula será normal, pero al llegar con velocidad nula, la aceleración vale cero. Por tanto se cumple
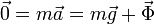
por tanto, la fuerza de reacción vincular compensa exactamente al peso
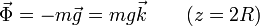
En el punto más bajo, tanto el peso como la reacción son normales al aro, con lo que la segunda ley de Newton nos da
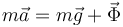

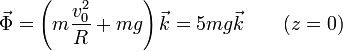
esto es, con la anilla en movimiento, el aro debe ejercer una fuerza igual a cinco veces el peso.
3 Bola
En el segundo caso tenemos una bola que se mueve en contacto con el aro, por el interior de éste, pero sin estar unida a él. Tenemos ahora un vínculo unilateral, ya que el aro puede impedir que el radio de la trayectoria supere el valor de R, pero no puede evitar que sea menor, esto es, que la partícula puede caerse al llegar a una cierta altura, ya que no hay nada que la retenga.
Matemáticamente, esto se manifiesta en que la fuerza de reacción vincular no puede tener los dos sentidos normales, sino solo uno de ellos. Siempre debe ir dirigida hacia adentro, nunca hacia afuera.
Esto implica que el resultado del apartado anterior no es aplicable a este caso, ya que la reacción vincular en el punto más alto no podría ir dirigida hacia arriba para retener la bolita. Lo que ocurriría al comunicarle esa velocidad es que llegado a una cierta altura, la bolita se separaría del aro y caería describiendo una parábola.
Si queremos que la partícula llegue hasta arriba debemos comunicarle una velocidad tal que la fuerza de reacción vincular se dirija hacia arriba, siendo el valor mínimo de la velocidad aquél que produce una reacción vincular nula.
Puesto que ahora la partícula llega con velocidad distinta de cero, la partícula posee una aceleración normal en el punto más alto, por lo que debe cumplirse
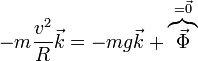
de donde la velocidad en el punto más alto cumple
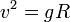
La velocidad en el punto inferior la obtenemos aplicando de nuevo la ley de conservación de la energía mecánica
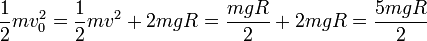
lo que nos da la nueva velocidad inicial
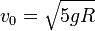
La reacción vincular en el punto más alto es nula, según hemos indicado

En el punto más bajo, de nuevo el peso y la reacción son normales al aro por lo que
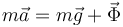

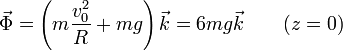
Ahora el aro debe ejercer una fuerza igual a seis veces el peso.





