2.3. Movimiento de partícula sujeta de un hilo

De Laplace

(Redirigido desde 3.3. Movimiento de partícula sujeta de un hilo)

Contenido

1 Enunciado
2 Ecuaciones horarias
3 Instante de máxima altura
4 Radio de curvatura

1 Enunciado

Una barra rígida $A B$ de longitud $L$ se mueve en un plano vertical $O X Y$ , manteniendo su extremo $A$ articulado en un punto del eje horizontal de coordenadas 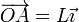$\overrightarrow{OA}= L \vec{\imath}$ , y verificando la ley horaria $θ(t) = 2ω t$ , con 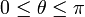$0 \leq \theta \leq \pi$ y siendo $ω =$ cte. Un hilo inextensible de longitud $2 L$ tiene uno de sus extremos conectado al origen del sistema de referencia (punto $O$ ), mientras que del otro cuelga una partícula $P$ que mantiene al hilo siempre tenso. El hilo se apoya sobre una pequeña polea de radio despreciable situada en el extremo $B$ de la barra, de forma que el tramo 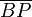$\overline{BP}$ permanece siempre paralelo al eje $O Y$ (ver figura). Se pide:

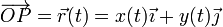Ecuaciones horarias del punto $P$ , $\overrightarrow{OP} = \vec{r}(t) =x(t) \vec{\imath} + y(t) \vec{\jmath}$ .
Instante del tiempo $t M$ en que la partícula alcanza su altura máxima.
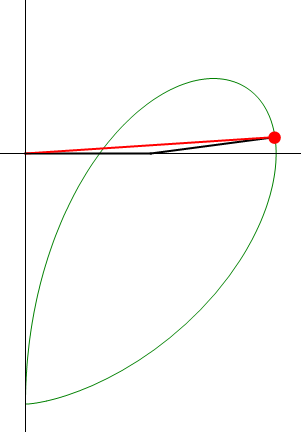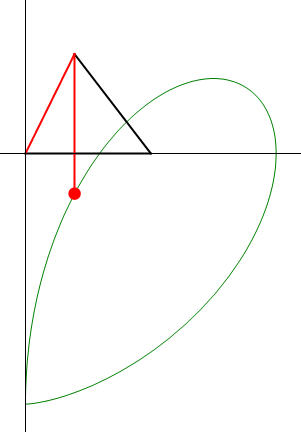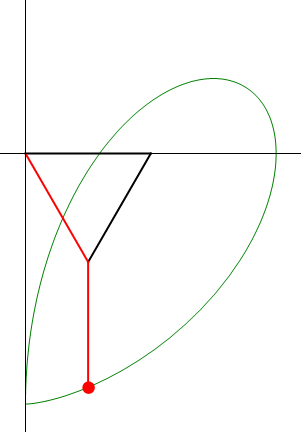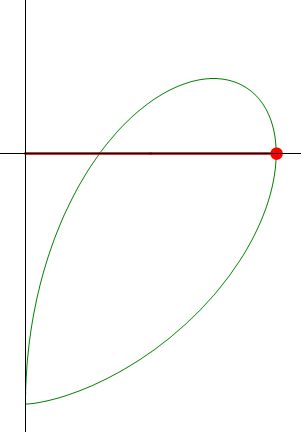
Radio de curvatura de la trayectoria seguida por $P$ , en el instante considerado en el apartado anterior.

2 Ecuaciones horarias

La posición del punto P puede escribirse como suma de tres vectores

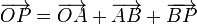
$\overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{AB}+\overrightarrow{BP}$

donde

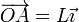
$\overrightarrow{OA}=L\vec{\imath}$

y

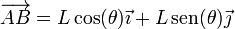
$\overrightarrow{AB}=L\cos(\theta)\vec{\imath}+L\,\mathrm{sen}(\theta)\vec{\jmath}$

El vector 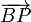$\overrightarrow{BP}$ es vertical hacia abajo y con un módulo igual a

$|\overrightarrow{BP}| = 2L-|\overrightarrow{OB}|$

siendo

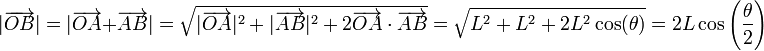
$|\overrightarrow{OB}| = |\overrightarrow{OA}+\overrightarrow{AB}| = \sqrt{|\overrightarrow{OA}|^2+|\overrightarrow{AB}|^2+2\overrightarrow{OA}\cdot\overrightarrow{AB}}=\sqrt{L^2+L^2+2L^2\cos(\theta)} = 2L\cos\left(\frac{\theta}{2}\right)$

Por tanto

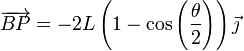
$\overrightarrow{BP}=-2L\left(1-\cos\left(\frac{\theta}{2}\right)\right)\vec{\jmath}$

y el vector de posición buscado es

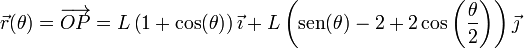
$\vec{r}(\theta)=\overrightarrow{OP} = L\left(1+\cos(\theta)\right)\vec{\imath}+L\left(\mathrm{sen}(\theta)-2+2\cos\left(\frac{\theta}{2}\right)\right)\vec{\jmath}$

En función del tiempo quedan las ecuaciones horarias

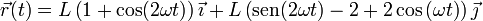
$\vec{r}(t) = L\left(1+\cos(2\omega t)\right)\vec{\imath}+L\left(\mathrm{sen}(2\omega t)-2+2\cos\left(\omega t\right)\right)\vec{\jmath}$

3 Instante de máxima altura

El instante de máxima altura se alcanza en el momento en que la componente vertical de la velocidad se anula.

La velocidad en cada instante es

$\vec{v}(t)=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=2L\omega\left[-\mathrm{sen}(2\omega t)\vec{\imath}+\left(\cos(2\omega t)-\mathrm{sen}(\omega t)\right)\vec{\jmath}\,\right]$

La componente $y$ se anula cuando

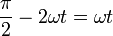
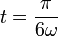
$0 = \cos(2\omega t)-\mathrm{sen}(\omega t) = \mathrm{sen}\left(\frac{\pi}{2}-2\omega t\right)-\mathrm{sen}(\omega t)$ $\Rightarrow$ $\frac{\pi}{2}-2\omega t = \omega t$ $\Rightarrow$ $t = \frac{\pi}{6\omega}$

Esto es, la máxima altura se alcanza cuando la barra forma un ángulo de π/3 = 60° con la horizontal.

4 Radio de curvatura

Para el radio de curvatura necesitamos la aceleración en ese instante. Derivando de nuevo

$\vec{a}(t)=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=-2L\omega^2\left[2\cos(2\omega t)\vec{\imath}+\left(2\,\mathrm{sen}(2\omega t)+\cos(\omega t)\right)\vec{\jmath}\,\right]$

En el instante de máxima altura, la aceleración vale

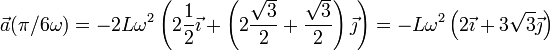
$\vec{a}(\pi/6\omega)=-2L\omega^2\left(2\frac{1}{2}\vec{\imath}+\left(2\frac{\sqrt{3}}{2}+\frac{\sqrt{3}}{2}\right)\vec{\jmath}\right) = -L\omega^2\left(2\vec{\imath}+3\sqrt{3}\vec{\jmath}\right)$

La velocidad en ese mismo instante es

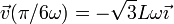
$\vec{v}(\pi/6\omega) = -\sqrt{3}L\omega\vec{\imath}$

Puesto que la velocidad es puramente horizontal, la aceleración normal es la componente vertical

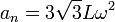
$a_n = 3\sqrt{3}L\omega^2$

Esto nos da el radio de curvatura

$R = \frac{v^2}{a_n}=\frac{3L^2\omega^2}{3L\omega^2\sqrt{3}}=\frac{1}{\sqrt{3}}L$

2.3. Movimiento de partícula sujeta de un hilo

De Laplace

Contenido

1 Enunciado

2 Ecuaciones horarias

3 Instante de máxima altura

4 Radio de curvatura

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES