Entrar Página Discusión Historial Go to the site toolbox

2.1. Ejemplo de movimiento plano en 3D

De Laplace

Contenido

1 Enunciado

Una partícula describe un movimiento según la ecuación horaria

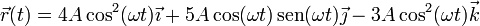
\vec{r}(t) = 4A\cos^2(\omega t)\vec{\imath}+5A\cos(\omega t)\,\mathrm{sen}(\omega t)\vec{\jmath}-3A\cos^2(\omega t)\vec{k}
  1. Calcule la velocidad y la aceleración instantáneas de este movimiento.
  2. Determine el parámetro arco como función del tiempo y escriba la ecuación de la trayectoria como función del parámetro arco.
  3. Calcule el triedro de Frenet asociado a la trayectoria en cada instante, así como las componentes intrínsecas de la aceleración
  4. Halle el radio de curvatura y la posición del centro de curvatura en cada instante. ¿Qué tipo de movimiento describe la partícula?

2 Velocidad y aceleración

2.1 Velocidad

Derivando una vez el vector de posición respecto al tiempo:

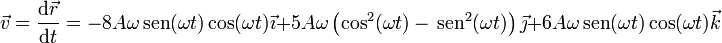
\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=-8A\omega\,\mathrm{sen}(\omega t)\cos(\omega t)\vec{\imath}+5A\omega\left(\cos^2(\omega t)-\,\mathrm{sen}^2(\omega t)\right)\vec{\jmath}+6A\omega\,\mathrm{sen}(\omega t)\cos(\omega t)\vec{k}

Podemos simplificar esta expresión con ayuda de las funciones trigonométricas del ángulo doble

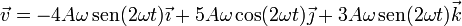
\vec{v}=-4A\omega\,\mathrm{sen}(2\omega t)\vec{\imath}+5A\omega\cos(2\omega t)\vec{\jmath}+3A\omega\,\mathrm{sen}(2\omega t)\vec{k}

2.2 Aceleración

Derivando de nuevo obtenemos el vector aceleración:

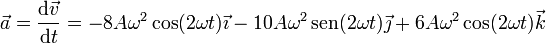
\vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=-8A\omega^2\cos(2\omega t)\vec{\imath}-10A\omega^2\,\mathrm{sen}(2\omega t)\vec{\jmath}+6A\omega^2\cos(2\omega t)\vec{k}

3 Parámetro arco

La celeridad nos da la derivada del parámetro arco respecto al tiempo. Hallamos el módulo de la velocidad

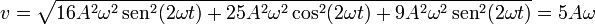
v = \sqrt{16A^2\omega^2\,\mathrm{sen}^2(2\omega t)+25A^2\omega^2\cos^2(2\omega t)+9A^2\omega^2\,\mathrm{sen}^2(2\omega t)}=5A\omega

Resulta que el movimiento es uniforme y el parámetro natural es proporcional al tiempo

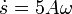
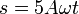
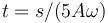
\dot{s}=5A\omega   \Rightarrow   s = 5A\omega t\,   \Rightarrow   t = s/(5A\omega)\,

y la ecuación de la trayectoria parametrizada naturalmente es

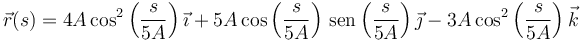
\vec{r}(s) = 4A\cos^2\left(\frac{s}{5A}\right)\vec{\imath}+5A\cos\left(\frac{s}{5A}\right)\,\mathrm{sen}\left(\frac{s}{5A}\right)\vec{\jmath}-3A\cos^2\left(\frac{s}{5A}\right)\vec{k}

4 Triedro de Frenet y componentes intrínsecas

4.1 Vector tangente

Obtenemos el vector tangente como el unitario en la dirección de la velocidad

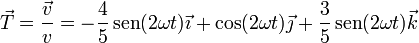
\vec{T}=\frac{\vec{v}}{v}=-\frac{4}{5}\,\mathrm{sen}(2\omega t)\vec{\imath}+\cos(2\omega t)\vec{\jmath}+\frac{3}{5}\,\mathrm{sen}(2\omega t)\vec{k}

4.2 Vector binormal

El binormal lo hallamos normalizando el producto vectorial de la velocidad y la aceleración

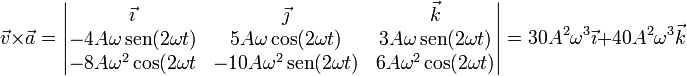
\vec{v}\times\vec{a}=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ -4A\omega\,\mathrm{sen}(2\omega t) & 5A\omega\cos(2\omega t) & 3A\omega\,\mathrm{sen}(2\omega t) \\ -8A\omega^2\cos(2\omega t & -10A\omega^2\,\mathrm{sen}(2\omega t) & 6A\omega^2\cos(2\omega t)\end{matrix}\right|=30A^2\omega^3\vec{\imath}+40A^2\omega^3\vec{k}

Dividiendo este vector por su módulo

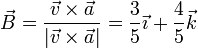
\vec{B}=\frac{\vec{v}\times\vec{a}}{|\vec{v}\times\vec{a}|}=\frac{3}{5}\vec{\imath}+\frac{4}{5}\vec{k}

Vemos que resulta un vector constante y por tanto la trayectoria es plana, aunque tenga las tres coordenadas dependientes del tiempo.

El plano que contiene a la trayectoria es el dado por la ecuación vectorial

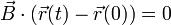
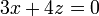
\vec{B}\cdot(\vec{r}(t)-\vec{r}(0)) = 0   \Rightarrow   3x+4z = 0\,

4.3 Vector normal

Conocidos el vector tangente y el vector binormal, hallamos el vector normal como su producto vectorial

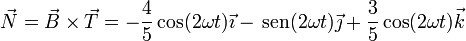
\vec{N}=\vec{B}\times\vec{T} = -\frac{4}{5}\cos(2\omega t)\vec{\imath}-\,\mathrm{sen}(2\omega t)\vec{\jmath}+\frac{3}{5}\cos(2\omega t)\vec{k}

4.4 Aceleración tangencial

Puesto que el movimiento es uniforme, la aceleración tangencial es nula

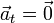
\vec{a}_t = \vec{0}

4.5 Aceleración normal

Si la aceleración tangencial es nula, en este caso toda la aceleración es normal

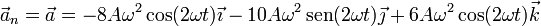
\vec{a}_n=\vec{a}=-8A\omega^2\cos(2\omega t)\vec{\imath}-10A\omega^2\,\mathrm{sen}(2\omega t)\vec{\jmath}+6A\omega^2\cos(2\omega t)\vec{k}

La componente normal de la aceleración la obtenemos proyectando la aceleración sobre el vector normal (o bien, en este caso, tomando simplemente el módulo de la aceleración ya que la componente normal es la única que hay y nunca puede ser negativa)

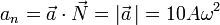
a_n = \vec{a}\cdot\vec{N} = |\vec{a}\,| = 10A\omega^2

Nótese también que la nulidad de la aceleración tangencial implica que se habría podido calcular el vector normal principal simplemente normalizando la aceleración y haber obtenido después el vector binormal como producto vectorial del tangente unitario y el normal.

5 Radio y centro de curvatura. Tipo de movimiento

5.1 Radio de curvatura

Hallamos el radio de curvatura a partir de la celeridad y la aceleración normal

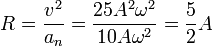
R = \frac{v^2}{a_n} = \frac{25A^2\omega^2}{10A\omega^2}=\frac{5}{2}A

5.2 Tipo de movimiento

Puesto que la trayectoria es plana (el vector binormal es constante) y el radio de curvatura es constante, llegamos a la conclusión de que se trata de un movimiento circular. Es más, dado que la rapidez es constante, el movimiento es circular uniforme.

5.3 Centro de curvatura

El centro de curvatura coincide en este caso con el centro de la circunferencia que describe la partícula

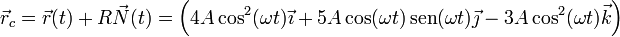
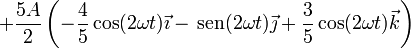
\vec{r}_c = \vec{r}(t) + R\vec{N}(t) = \left(4A\cos^2(\omega t)\vec{\imath}+5A\cos(\omega t)\,\mathrm{sen}(\omega t)\vec{\jmath}-3A\cos^2(\omega t)\vec{k}\right)+\frac{5A}{2}\left(-\frac{4}{5}\cos(2\omega t)\vec{\imath}-\,\mathrm{sen}(2\omega t)\vec{\jmath}+\frac{3}{5}\cos(2\omega t)\vec{k}\right)

Desarrollando las funciones trigonométricas del ángulo doble, queda finalmente

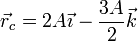
\vec{r}_c = 2A\vec{\imath}- \frac{3A}{2}\vec{k}

que efectivamente es un punto fijo, como corresponde a un movimiento circular.

Obtenido de "http://tesla.us.es/wiki/index.php/2.1._Ejemplo_de_movimiento_plano_en_3D"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 21:28, 17 oct 2020. - Esta página ha sido visitada 18.763 veces. - Aviso legal - Acerca de Laplace