Disco y varilla con dos rotaciones
De Laplace
Contenido |
1 Enunciado
El sistema de la figura está formado por una varilla AB de longitud l (sólido "0"), cuyo extremo A está fijado en el eje vertical O1Z1, a una altura R sobre el plano horizontal fijo O1X1Y1 (sólido "1"). La varilla AB gira alrededor de O1Z1 con una velocidad angular constante Ω, permaneciendo siempre perpendicular a dicho eje vertical fijo. El extremo B del sólido "0" está articulado al centro de un disco de radio R (sólido "2"), de modo que la varilla es siempre perpendicular al disco. El disco gira con una velocidad angular constante ω, coincidiendo su eje de giro con la varilla.
- Caracteriza los movimientos {01}, {20} y {21} (reducciones cinemáticas).
- Obtén la expresión de la velocidad
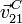del punto de contacto del disco con el plano fijo O1X1Y1, (punto C) en término de los datos del problema. ¿Qué relación debe existir entre las velocidades angulares ω y Ω para que el disco ruede sin deslizar sobre el plano?
- Obtén las expresiones de la aceleración angular del movimiento {21} y de la aceleración
del centro del disco (punto B). Calcula la aceleración del punto de contacto C perteneciente al disco cuando éste rueda sin deslizar sobre el plano O1X1Y1.
2 Solución
2.1 Reducciones cinemáticas
2.1.1 Movimiento {01}
Es una rotación de eje permanente. El eje de rotación es O1Z1. Reduciendo en el punto O1 tenemos
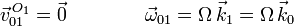
2.1.2 Movimiento {20}
El centro del disco pertenece siempre a los dos sólidos "2" y "0". Por tanto es un punto fijo del movimiento. La velocidad angular es ω, dirigida a lo largo de la varilla. Reduciendo en el punto B tenemos
2.1.3 Movimiento {21}
Expresamos este movimiento como la composición
{21} = {20} + {01}
La velocidad angular es
