Rapidez y tensión de un péndulo

De Laplace

Revisión a fecha de 13:40 27 nov 2011; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Solución

1 Enunciado

Halle el error relativo cometido al calcular la velocidad para un péndulo en su punto más bajo empleando la aproximación de oscilador armónico, si se suelta en reposo desde un ángulo respecto a la vertical de (a) 1° (b) 10° (c) 30° (d) 60° (e) 90°.

2 Solución

2.1 Valor aproximado

Un péndulo obedece la ecuación de movimiento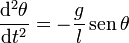 $\frac{\mathrm{d}^2\theta}{\mathrm{d}t^2}=-\frac{g}{l}\,\mathrm{sen}\,\theta$

siendo $θ$ la inclinación respecto a la vertical (medida en radianes). Cuando esta separación es pequeña, se puede usar la aproximación

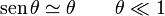
$\mathrm{sen}\,\theta\simeq\theta \qquad\theta\ll 1$

lo que reduce la ecuación del péndulo a la de un oscilador armónico

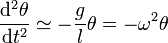
$\frac{\mathrm{d}^2\theta}{\mathrm{d}t^2}\simeq-\frac{g}{l}\theta=-\omega^2\theta$

Cuando parte del reposo, desde una cierta separación $θ 0$ , el ángulo sigue una ley cosenoidal

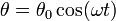
$\theta = \theta_0\cos(\omega t)\,$

La velocidad lineal de la lenteja del péndulo es

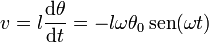
$v = l\frac{\mathrm{d}\theta}{\mathrm{d}t} = -l\omega\theta_0\,\mathrm{sen}(\omega t)$

El valor máximo (en módulo) de esta velocidad lo alcanza en el momento en que se encuentra en el punto más bajo

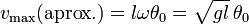
$v_\mathrm{max}(\mathrm{aprox.})=l\omega\theta_0= \sqrt{gl}\,\theta_0$

2.2 Valor exacto

Esta misma velocidad puede calcularse exactamente, empleando la ley de conservación de la energía mecánica.

La energía inicial, cuando parte del reposo, es puramente potencial. Tomando el origen de alturas en el punto más bajo de la trayectoria

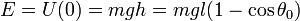
$E = U(0) = mg h = mgl(1-\cos\theta_0)\,$

La energía en el punto más bajo es puramente cinética

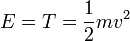
$E = T = \frac{1}{2}mv^2$

Igualando estas dos cantidades

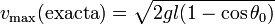
$v_\mathrm{max}(\mathrm{exacta}) = \sqrt{2gl(1-\cos\theta_0)}$

2.3 Comparación

El cociente entre el valor aproximado y el exacto es

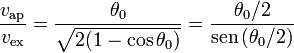
$\frac{v_\mathrm{ap}}{v_\mathrm{ex}} = \frac{\theta_0}{\sqrt{2(1-\cos\theta_0)}} = \frac{\theta_0/2}{\mathrm{sen}\,(\theta_0/2)}$

donde hemos empleado la fórmula del ángulo mitad. Dado que

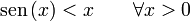
$\mathrm{sen}\,(x) < x\qquad \forall x > 0$

esto quiere decir que la aproximación de oscilador armónico predice una velocidad mayor que la real. El periodo calculado con esta aproximación será entonces más pequeño que el exacto.

El error relativo cometido en la aproximación es

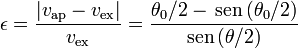
$\epsilon = \frac{|v_\mathrm{ap}-v_\mathrm{ex}|}{v_\mathrm{ex}} = \frac{\theta_0/2-\,\mathrm{sen}\,(\theta_0/2)}{\mathrm{sen}\,(\theta/2)}$

Aplicando esta fórmula a los ángulos del enunciado

$θ 0$ (°)	$θ 0$ (rad)	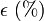$\epsilon\ (\%)$
1	π/180	0.00127
10	π/10	0.127
30	π/6	1.15
60	π/3	4.72
90	π/2	11.07

Vemos que, en general la aproximación es bastante buena y que incluso para ángulos tan grandes como 60° el error es inferior al 5 %.

Rapidez y tensión de un péndulo

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Valor aproximado

2.2 Valor exacto

2.3 Comparación

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES