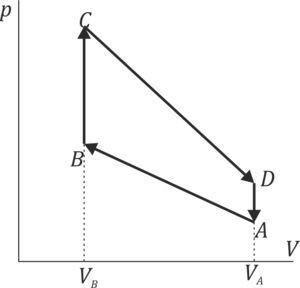
Ciclo termodinámico trapezoidal (GIE)
De Laplace
(Diferencias entre revisiones)
(→Trabajo para cualquier pB) |
(→Trabajo para cualquier pB) |
||
| Línea 14: | Línea 14: | ||
==Trabajo para cualquier ''p''<sub>''B''</sub>== | ==Trabajo para cualquier ''p''<sub>''B''</sub>== | ||
Área de un trapecio | Área de un trapecio | ||
| - | <math>W=\frac{p_A+p_B}{2}(V_A-V_B)=40.8+0.4p_B</math> | + | <center><math>W=\frac{p_A+p_B}{2}(V_A-V_B)=40.8+0.4p_B</math></center> |
(<math>p_B</math> en kPa, <math>W</math> en J) | (<math>p_B</math> en kPa, <math>W</math> en J) | ||
Revisión de 19:16 20 mar 2017
Contenido |
1 Enunciado
Una cierta cantidad de aire seco experimenta una compresión cuasiestática A→B que se describe en un diagrama pV con un segmento rectilíneo como el de la figura. Sean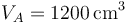 
, 
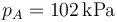y 
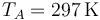las condiciones iniciales yVA / VB = r = 3 la relación de compresión
- Calcule el trabajo realizado sobre el sistema en el proceso A→B como función de la presión final pB y del resto de datos del problema.
- Halle el valor de la presión final pB si en el proceso descrito el calor neto que entra en el sistema es nulo,
.
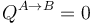- Halle la temperatura final T_B en el proceso anterior.
Suponga ahora un ciclo similar al Otto en el que el proceso A→B es el del apartado 2 y el C→D es del mismo tipo (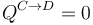
) con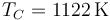 
. Los procesos B→C y D→A son isócoros.
- Halle la presión, temperatura y volumen de los estados A, B, C y D.
- Calcule el calor, el trabajo y la variación de la energía interna en cada uno de los procesos.
2 Trabajo para cualquier pB
Área de un trapecio
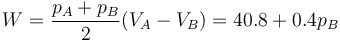
(pB en kPa, W en J)
