Problemas de Gas Ideal
De Laplace
(→Ecuación de Van der Waals) |
(→Ecuación de Van der Waals) |
||
| Línea 114: | Línea 114: | ||
[[Ecuación de Van der Waals|'''Solución''']] | [[Ecuación de Van der Waals|'''Solución''']] | ||
| + | |||
| + | ==[[Compresión lineal]]== | ||
| + | Se tiene un volumen <math>V_0</math> de un gas ideal diatómico a una presión <math>p_0</math> y una temperatura <math>T_0</math> encerrado en un recipiente con un pistón móvil. Este gas se comprime reversiblemente según la ley | ||
| + | |||
| + | <center><math>p = 3p_0-\frac{2p_0V}{V_0}</math></center> | ||
| + | |||
| + | reduciéndose el volumen hasta <math>V_0/2</math>. | ||
| + | |||
| + | # Trace la gráfica del proceso en un diagrama PV. | ||
| + | # Calcule la temperatura final del proceso. | ||
| + | # Calcule el trabajo neto realizado sobre el gas, la variación de su energía interna y el calor que entra en el gas durante el proceso. | ||
| + | # ¿Para qué volumen durante el proceso la temperatura es máxima? Halle el valor de esta temperatura máxima. | ||
| + | # Separando el proceso en dos: uno hasta que alcanza la temperatura máxima y otro de ahí hasta el final, halle <math>W</math>, <math>\Delta U</math> y <math>Q</math> en cada uno de los dos subprocesos. | ||
== Otros problemas == | == Otros problemas == | ||
última version al 16:09 16 nov 2010
1 Ecuación de estado
Utilizando la ecuación de estado de los gases ideales, responda a las siguientes preguntas
- ¿Que volumen ocupa un mol de gas en condiciones estándar?
- ¿Cuantas moléculas hay en
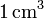de gas ideal a una temperatura de 300 K y a una presión de 1 atm?
¿Y si la presión es de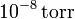 
?
2 Pistón oscilante
Un cilindro de 2.40 m de altura se llena con 0.100 moles de un gas ideal a una temperatura de 25oC y una presión de 1 bar. El cilindro se cierra entonces con un pistón de masa 1.40 kg que se deja caer hasta alcanzar el equilibrio.
- Determine la altura h0 del pistón suponiendo que la temperatura del gas no varía en la compresión.
- Suponga que el pistón se empuja ligeramente hacia abajo más allá de la posición de equilibrio y luego se libera. Suponiendo que la temperatura del gas permanece constante y que el rozamiento del pistón es despreciable, demuestre que el pistón describe aproximadamente un movimiento armónico simple y determine su frecuencia.
- Suponga ahora que el cilindro posee paredes adiabáticas, de forma que la temperatura del gas ya no permanecerá constante. Si la posición de equilibrio se supone que es la misma del primer apartado, ¿cuál será, en este caso, la frecuencia de las oscilaciones?
3 Trabajo en distintos procesos
Un mol de un gas ideal está contenido en un cilindro que tiene un émbolo móvil. La presión, volumen y temperatura iniciales son Pi,Vi,Ti, respectivamente. Calcule el trabajo realizado sobre el gas para los siguientes procesos, y dibuje cada uno de ellos en un diagrama PV
- Una compresión isobárica en la que el volumen final sea la mitad del volumen inicial
- Una compresión isotérmica en la que la presión final se cuatro veces la inicial
- Un proceso isócoro en el que la presión final sea el triple de la inicial.
4 Trabajo en un ciclo
Las condiciones iniciales del estado de un gas perfecto son: V=4 l, P=2 atm, t = 27o C. Se dilata el gas a presión constante hasta duplicar su volumen. A continuación se comprime isotérmicamente hasta recuperar el volumen inicial. Finalmente se enfría a volumen constante hasta su presión inicial.
- Dibuje el ciclo en un diagrama PV.
- Calcule el trabajo realizado sobre el gas en el ciclo suponiendo que los procesos son cuasiestáticos.
5 Termómetro con dos cámaras
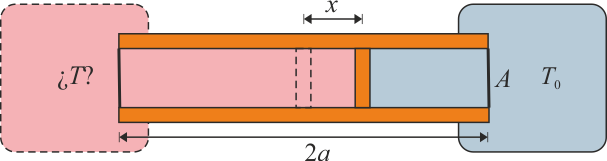
Se construye un termómetro de gas ideal según el siguiente principio: un tubo cilíndrico de sección S y longitud 2a con paredes adiabáticas y bases diatermas es dividido por un pistón, también adiabático, que puede deslizarse sin rozamiento por el interior del tubo. En el interior de las dos cámaras se encuentra un gas ideal. Una de las dos cámaras se mantiene en contacto térmico con un foco a temperatura T0, mientras que la otra se pone en contacto con el sistema cuya temperatura se quiere medir. Cuando las dos temperaturas son iguales el pistón se encuentra en la posición central y la presión del gas es p0.
- Calcule la temperatura absoluta T a la que se encuentra el sistema cuando el pistón se ha desplazado una cantidad x desde el centro hacia el sistema a T0. ¿Resulta una escala lineal de temperaturas? ¿A cuánto tiende x si
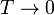o si 
?
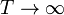- Supongamos que se parte del equilibrio a T0 y que la variación de la temperatura del gas de la cámara exterior y el desplazamiento del pistón en x ha sido de forma cuasiestática y reversible. ¿Cuáles son los calores, trabajos e incrementos de energía interna para cada una de las cámaras y para el tubo completo, como función del desplazamiento x del pistón?
- Supongamos que el tubo mide 20 cm, la temperatura de referencia es T0 = 300 K y el pistón se desplaza 1 cm. ¿Cuál es la temperatura del sistema exterior?
- Si además sabemos que la sección del tubo es de 10 cm2 , el gas contenido es aire y la presión inicial es p0 = 100 kPa, ¿cuánto valen los calores, trabajos e incrementos de energía interna del segundo apartado?
Dato: La constante de los gases ideales es R = 8.314 J/mol · K.
6 Comparación de un proceso isotérmico y uno adiabático
Un gas ideal monoatómico ocupa un volumen de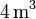 
a la presión de 
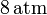y a la temperatura de
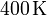. El gas se expande hasta la presión final de
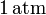mediante un proceso cuasiestático. Calcule el
trabajo realizado, el calor absorbido y la variación de energía interna en
los siguientes casos:
- Expansión isoterma.
- Expansión adiabática.
7 Proceso isotermo y adiabático consecutivos
Se comprime un mol de aire en condiciones estándar mediante un proceso isotermo hasta reducir su volumen a la mitad, luego se expande adiabáticamente hasta recuperar su presión inicial. Ambos procesos son cuasiestáticos. Halle
- La temperatura final
- El trabajo total realizado por el gas
- El calor total absorbido por el gas
- La variación de energía interna
8 Expansión adiabática no cuasiestática
4 moles de nitrógeno están a 25°C y 30 atm. Se pasa bruscamente la presión hasta un valor de 10 atm mediante una expansión adiabática del gas contra una presión exterior constante de 10 atm. El proceso no es cuasiestático. Calcule
- La temperatura final del gas suponiendo que la ecuación de estado de los gases ideales es aplicable a los estados inicial y final.
- La variación de energía interna.
- El trabajo realizado sobre el gas.
- Compare con las mismas magnitudes en un proceso adiabático cuasiestático que expanda el gas hasta la misma presión final de 10 atm.
9 Presión en una mezcla de gases
En un frasco de 10 litros se mezclan 2 litros del gas A a 3 atmósferas de presión y 3 litros del gas B a 5 atmósferas. Admitiendo que los gases son ideales e inertes, ¿cuál será la presión final si la temperatura permanece constante en todo el proceso?
10 Ecuación de Van der Waals
El comportamiento del gas butano se ajusta, dentro de ciertos límites, a la ecuación de estado de Van der Waals
siendo en este caso a = 14.5 atm·l² y b = 0.122 l. Calcule el trabajo realizado por un mol de gas butano, considerándolo como un gas de Van der Waals, al expansionarse cuasiestáticamente desde 2 l hasta 3 l a la temperatura constante de t = 27°C. Compare con el resultado que daría la ecuación de los gases ideales.
11 Compresión lineal
Se tiene un volumen V0 de un gas ideal diatómico a una presión p0 y una temperatura T0 encerrado en un recipiente con un pistón móvil. Este gas se comprime reversiblemente según la ley
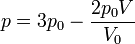
reduciéndose el volumen hasta V0 / 2.
- Trace la gráfica del proceso en un diagrama PV.
- Calcule la temperatura final del proceso.
- Calcule el trabajo neto realizado sobre el gas, la variación de su energía interna y el calor que entra en el gas durante el proceso.
- ¿Para qué volumen durante el proceso la temperatura es máxima? Halle el valor de esta temperatura máxima.
- Separando el proceso en dos: uno hasta que alcanza la temperatura máxima y otro de ahí hasta el final, halle W, ΔU y Q en cada uno de los dos subprocesos.
