Problemas de dinámica del sólido rígido (GIOI)
De Laplace
(→Bola que rueda por una pendiente) |
(→Barra apoyada con resorte) |
||
| (3 ediciones intermedias no se muestran.) | |||
| Línea 11: | Línea 11: | ||
[[Momento de inercia de un sistema de partículas|Solución]] | [[Momento de inercia de un sistema de partículas|Solución]] | ||
| + | |||
| + | ==Centro de masas de un triángulo== | ||
| + | Se tiene una chapa delgada y homogénea en forma de triángulo de vértices en los puntos A, B y C. ¿Dónde se encuentra su centro de masas? | ||
| + | |||
| + | [[Centro de masas de un triángulo|Solución]] | ||
==Momento de inercia de sólidos esféricos== | ==Momento de inercia de sólidos esféricos== | ||
| Línea 51: | Línea 56: | ||
[[Equilibrio de una barra apoyada|Solución]] | [[Equilibrio de una barra apoyada|Solución]] | ||
| + | |||
| + | ==Barra apoyada con resorte== | ||
| + | Se tiene un sistema formado por una varilla de masa <math>m=1.2 kg</math> y longitud <math>\ell_0=1 m</math>, apoyada sin rozamiento en una pared vertical y un suelo horizontal. El extremo B, apoyado en la pared, está conectado a la esquina mediante un resorte de constante <math>k=30N/m</math> y longitud natural <math>\ell_0=1 m</math>. Por efecto de la gravedad (tómese <math>g=10 m/s^2</math>) la varilla tiende a bajar, pero el resorte la empuja hacia arriba, existiendo una posición de equilibrio. | ||
| + | |||
| + | <center>[[Archivo:barra-apoyada-resorte.png|300px]]</center> | ||
| + | # Determine la posición de los extremos A y B de la barra en la posición de equilibrio. | ||
| + | # Halle las fuerzas de reacción en la pared y en el suelo en esta posición de equilibrio. | ||
| + | # Suponga ahora que la barra se sitúa inicialmente en la posición vertical en reposo. Se le comunica un ligerísimo impulso, de manera que comienza a resbalar. | ||
| + | ## Calcule la posición de A y B en el momento en que el muelle se comprime al máximo (a partir del cual la barra vuelve a subir). | ||
| + | ## Durante el descenso, la barra pasa (en movimiento) por la posición de equilibrio. Calcule la velocidad de A, de B y del centro de masas, G, en ese instante. | ||
| + | |||
| + | [[Barra apoyada con resorte (GIOI)|Solución]] | ||
==Fuerza sobre una barra== | ==Fuerza sobre una barra== | ||
última version al 11:07 22 nov 2020
1 Momento de inercia de un sistema de partículas
Se tiene un sólido formado por ocho partículas de masa m situadas en los vértices de un cubo de arista b.
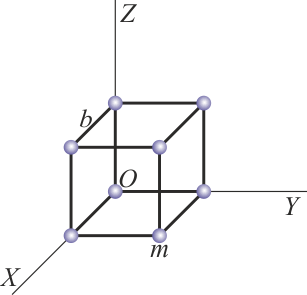
Halle el momento de inercia del cubo respecto a los siguientes ejes:
- Uno perpendicular a una cara y que pase por el centro del cubo.
- Uno que pase por dos vértices opuestos.
- Uno que pase por los centros de dos aristas opuestas.
- Uno que pase por una arista
2 Centro de masas de un triángulo
Se tiene una chapa delgada y homogénea en forma de triángulo de vértices en los puntos A, B y C. ¿Dónde se encuentra su centro de masas?
3 Momento de inercia de sólidos esféricos
Calcule el momento de inercia de una esfera maciza, de masa M y radio R alrededor de de un eje que pasa por su centro.
A partir del resultado anterior, halle el momento de inercia de una esfera hueca, de masa M, radio interior R1 y exterior R2 respecto a un eje que pasa por su centro. ¿A qué se reduce el resultado cuando la corona se reduce a una superficie esférica de radio R?
4 Momento de inercia de sólidos cilíndricos
Halle los siguientes momentos de inercia de sólidos de densidad homogénea:
- Una superficie cilíndrica hueca, de masa M, radio R y altura H.
- Un cilindro macizo, de masa M, radio R y altura H.
- Una corona cilíndrica de masa M, radio interior R1 y exterior R2, con altura H
En todos los casos, el momento de inercia debe hallarse respecto al eje del cilindro.
5 Barra sujeta por un cable
Una mesa plegable está articulada a la pared por un extremo, y cuelga de la pared por un cable tirante. En dos dimensiones esto se puede modelar como una barra de longitud b y masa m distribuida uniformemente. La barra está articulada por su extremo A y atada por su extremo B a una pared vertical, de forma que el cable forma un ángulo de 45° con la vertical.
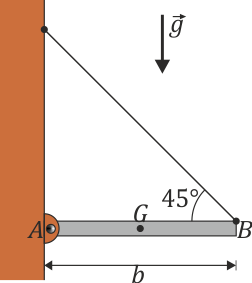
Calcule la tensión del cable, así como la fuerza de reacción en el punto A.
6 Movimiento de una mancuerna ideal
Supongamos dos masas iguales m unidas por una barra rígida de longitud b, sin masa (lo que sería una mancuerna ideal). Las masas reposan sobre un plano horizontal, sobre el que pueden moverse sin rozamiento. A una de las masas se le comunica una velocidad inicial  perpendicular a la línea de la barra, mientras que la otra se encuentra inicialmente en reposo. ¿Cuánto valen la cantidad de movimiento, el momento cinético respecto al CM y la energía cinética de la barra? ¿Cómo es el movimiento del sistema a partir de ese momento?
perpendicular a la línea de la barra, mientras que la otra se encuentra inicialmente en reposo. ¿Cuánto valen la cantidad de movimiento, el momento cinético respecto al CM y la energía cinética de la barra? ¿Cómo es el movimiento del sistema a partir de ese momento?
7 Equilibrio de una barra apoyada
Supongamos que tenemos una barra de masa M y longitud b apoyada en el suelo y en una pared vertical.
- Suponga primero que no hay rozamiento con las superficies y que la barra forma un ángulo θ con la vertical. ¿Puede quedarse en equilibrio la barra para algún valor de θ?
- Suponga ahora que la barra posee un coeficiente de rozamiento estático μ con el suelo. ¿Para qué ángulos puede alcanzarse entonces el equilibrio?
8 Barra apoyada con resorte
Se tiene un sistema formado por una varilla de masa m = 1.2kg y longitud 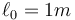 , apoyada sin rozamiento en una pared vertical y un suelo horizontal. El extremo B, apoyado en la pared, está conectado a la esquina mediante un resorte de constante k = 30N / m y longitud natural
, apoyada sin rozamiento en una pared vertical y un suelo horizontal. El extremo B, apoyado en la pared, está conectado a la esquina mediante un resorte de constante k = 30N / m y longitud natural 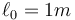 . Por efecto de la gravedad (tómese g = 10m / s2) la varilla tiende a bajar, pero el resorte la empuja hacia arriba, existiendo una posición de equilibrio.
. Por efecto de la gravedad (tómese g = 10m / s2) la varilla tiende a bajar, pero el resorte la empuja hacia arriba, existiendo una posición de equilibrio.
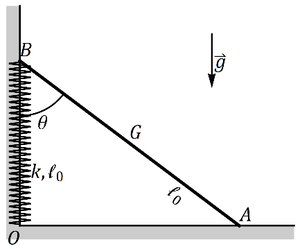
- Determine la posición de los extremos A y B de la barra en la posición de equilibrio.
- Halle las fuerzas de reacción en la pared y en el suelo en esta posición de equilibrio.
- Suponga ahora que la barra se sitúa inicialmente en la posición vertical en reposo. Se le comunica un ligerísimo impulso, de manera que comienza a resbalar.
- Calcule la posición de A y B en el momento en que el muelle se comprime al máximo (a partir del cual la barra vuelve a subir).
- Durante el descenso, la barra pasa (en movimiento) por la posición de equilibrio. Calcule la velocidad de A, de B y del centro de masas, G, en ese instante.
9 Fuerza sobre una barra
Sobre una barra de longitud b y masa M situada en reposo horizontalmente en una superficie sin rozamiento se aplica una fuerza F0 también horizontal. El punto de la aplicación se encuentra a una distancia c del centro de la barra.
- Si la fuerza es perpendicular a la barra, ¿cuánto valen la aceleración del CM y la aceleración angular de la barra? ¿Alrededor de qué punto comienza a girar la barra?
- Suponga ahora que la fuerza forma un ángulo β con la barra, ¿cuánto valen ese caso las aceleraciones y donde se encuentra el centro instantáneo de rotación?
- Suponga que la barra se encuentra articulada en un extremo de forma que sólo puede girar en torno a este punto. ¿Cuánto valen las aceleraciones en ese caso? ¿Cuánto vale la fuerza que el punto de articulación ejerce sobre la barra?
- Si la barra estuviera empotrada en su extremo, de forma que no pudiera moverse de ninguna manera, ¿cuánto valdrían la fuerza y el momento de reacción ejercidos por el soporte?
10 Equilibrio de una tabla
Se tiene una plataforma de masa 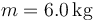 y longitud
y longitud  (estando la masa distribuida uniformemente) que se apoya horizontalmente sobre dos caballetes de forma que los puntos de apoyo A y B están a 60 cm y 20 cm del centro C de la tabla, respectivamente.
(estando la masa distribuida uniformemente) que se apoya horizontalmente sobre dos caballetes de forma que los puntos de apoyo A y B están a 60 cm y 20 cm del centro C de la tabla, respectivamente.
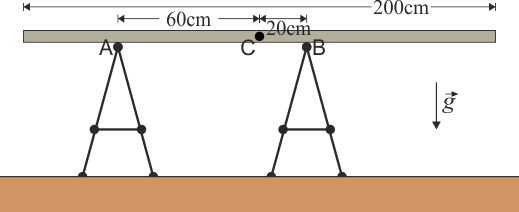
- Calcule la fuerza que cada caballete ejerce sobre la tabla.
- Halle el valor máximo de la masa que se puede apoyar en el borde izquierdo de la plataforma si no se quiere que esta vuelque.
- Suponga que sobre el extremo derecho de la plataforma se apoya una masa de 2.2 kg. ¿Volcará la tabla? Si es así, determine la aceleración angular que adquiere la tabla el comenzar a girar en torno al punto de apoyo, así como la fuerza que ejerce ese caballete sobre la mesa en el instante en que empieza a volcar.
Tómese 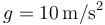 .
.
Dato: Momento de inercia de una barra de masa m y longitud b respecto a un eje perpendicular a ella y que pasa por su centro: I = mb2; / 12.
11 Barra apoyada en bloque
Una barra homogénea de 10 N de peso y 150 cm de longitud está articulada por uno de sus extremos, O. La barra está apoyada sin rozamiento sobre un bloque cuadrado homogéneo de h = 60cm de lado y 9.6 N de peso fijado al suelo, de manera que su borde está a 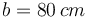 de O. Sea A el punto del bloque donde se apoya la barra.
de O. Sea A el punto del bloque donde se apoya la barra.

- Determine la fuerza que se ejerce sobre la barra en O y en A.
Suponga ahora que el bloque no está soldado al suelo, sino solo apoyado en él, y es mantenido en su posición por la fuerza de rozamiento estático.
- Calcule la resultante de las fuerzas de reacción que el suelo ejerce sobre el bloque.
- Determine el valor mínimo del coeficiente de rozamiento μ para que el sistema se quede en equilibrio.
- Halle el momento resultante de las fuerzas de reacción del suelo sobre el bloque respecto a la esquina B de éste.
12 Péndulo compuesto
Se tiene un péndulo compuesto consistente en una barra de longitud b y masa M suspendida por un punto situado a una distancia d del centro de la barra (d < b / 2). Suponiendo que la barra se desvía un ángulo pequeño θ0 respecto de la vertical y a partir de ahí se suelta:
- Determine el periodo de oscilación de la barra
- Suponga ahora que la barra se sitúa horizontalmente y desde ahí se suelta. Para el instante en que pasa por la vertical, calcule:
- La velocidad angular de la barra y la velocidad lineal de los extremos de la barra.
- Calcule la fuerza ejercida sobre el punto de anclaje.
- Calcule la tensión en cada punto de la barra.
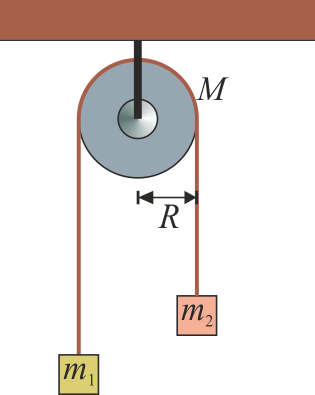
13 Máquina de Atwood con polea pesada
Dos masas m1 y m2 están unidas por una cuerda ideal, inextensible y sin masa. Esta cuerda pasa por una polea de masa M, que se puede modelar como un cilindro de radio R. La polea no tiene rozamiento que le impida girar en torno a su eje. Determine la aceleración con la que se mueven las masas, las tensiones en cada tramo de la cuerda, así como la fuerza en el punto de anclaje de la polea.
14 Rodadura por una pendiente
En lo alto de un plano inclinado de altura h y con una cierta pendiente se encuentran los siguientes objetos
- Una superficie cilíndrica hueca
- Un cilindro macizo
- Una superficie esférica hueca
- Una esfera maciza
Si se sueltan a la vez desde el extremo superior del plano, ¿dependerá el orden de llegada de la masa y el radio de cada uno? ¿con qué rapidez del CM llega cada uno al punto más bajo del plano? ¿en qué orden llegarán y cuanto tarda cada uno en llegar? Si además se suelta un bloque que desliza sin rozamiento por el plano, ¿llegará antes o después que los objetos rodantes? ¿Cuánto?
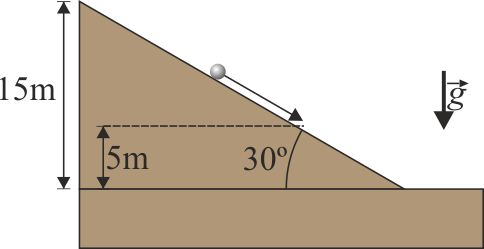
15 Bola que rueda por una pendiente
Una esfera metálica de acero con radio 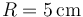 ) se encuentra inicialmente en reposo a una altura
) se encuentra inicialmente en reposo a una altura 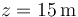 y desciende rodando sin deslizar por el plano inclinado con un ángulo
y desciende rodando sin deslizar por el plano inclinado con un ángulo 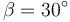 . El coeficiente de rozamiento estático entre el plano y el cilindro es μ. El rozamiento por rodadura es despreciable.
. El coeficiente de rozamiento estático entre el plano y el cilindro es μ. El rozamiento por rodadura es despreciable.
- ¿Qué relación existe entre la aceleración angular de la esfera y la lineal de su centro de masas?
- ¿Cuánto valen la energía cinética de rotación, la cinética de traslación, la potencial (tomando z = 0 como referencia) y la mecánica cuando se halla en
 ?
?
- ¿Cuánto vale, en módulo, la aceleración lineal del centro de masas de la esfera?
- ¿Cuál es el valor mínimo que debe tener el coeficiente de rozamiento μ si la esfera rueda sin deslizar?
Dato: Momento de inercia de una esfera de masa M y radio R respecto a un eje que pasa por su centro: I = (2 / 5)MR2. Aceleración de
la gravedad 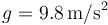 . Densidad de masa del acero:
. Densidad de masa del acero:  .
.
16 Rodadura con rozamiento dinámico
Por un suelo horizontal se lanza un disco macizo de masa m y radio R. Inicialmente el centro del disco avanza con velocidad 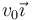 y el disco gira con velocidad angular \omega_0 \vec{k}, de manera que desliza además de rodar. El coeficiente de rozamiento dinámico con el suelo vale μ.
y el disco gira con velocidad angular \omega_0 \vec{k}, de manera que desliza además de rodar. El coeficiente de rozamiento dinámico con el suelo vale μ.
- Determine la aceleración lineal del centro del disco y la aceleración angular del disco.
- Halle la velocidad lineal del centro del disco, la velocidad angular del disco y la velocidad lineal del disco en el punto de contacto con el suelo como funciones del tiempo
- ¿Cuánto tarda el disco en dejar de deslizar y empezar a rodar sin deslizar?
- ¿Cómo es el movimiento una vez que empieza a rodar sin deslizar? ¿Cuál debe ser la velocidad angular inicial mínima para que el disco retorne al lanzador?
- Estudie como varían en el tiempo la energía cinética de traslación, de rotación y la total.





