Segunda Prueba de Control 2017/18 (G.I.C.)
De Laplace
(Diferencias entre revisiones)
(Página creada con '== Onda viajera en una cuerda tensa == Una onda viajera en una cuerda tensa está descrita por la expresión <center> <m…') |
(→Onda viajera en una cuerda tensa) |
||
| Línea 1: | Línea 1: | ||
| + | ==[[ Partícula en plano inclinado con dos muelles (Ene. 2018 G.I.C.)| Partícula en plano inclinado con dos muelles ]]== | ||
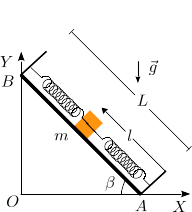
| + | [[Imagen:F1CIC_ParticulaPlanoMuelles_Enunciado.png|right]] | ||
| + | Una masa <math>m</math> desliza sin rozamiento sobre un plano inclinado un ángulo <math>\beta</math> | ||
| + | respecto a la horizontal. La barra está conectada a dos muelles ideales como se | ||
| + | indica en la figura. Los muelles tienen constante elástica <math>k</math> y longitud | ||
| + | natural nula. El muelle se ajusta de modo que <math>k=mg/L</math>. El ángulo <math>\beta</math> cumple | ||
| + | <center> | ||
| + | <math> | ||
| + | \,\mathrm{sen}\,\beta= 3/5, \qquad \cos\beta= 4/5. | ||
| + | </math> | ||
| + | </center> | ||
| + | #Escribe la expresión que da la energía mecánica de la partícula para cualquier punto del plano. | ||
| + | #En el instante inicial la partícula está en el punto <math>A</math> y se le comunica una velocidad de módulo <math>v_0</math> dirigida hacia arriba. ¿Que valor mínimo debe tener <math>v_0</math> para que la partícula llegue hasta el punto B? | ||
| + | #Repite el cálculo del apartado anterior si hay un rozamiento entre la partícula y el plano con coeficiente de rozamiento dinámico <math>\mu=0.5</math>. | ||
| + | |||
| + | |||
==[[ Onda viajera en una cuerda tensa (Nov. 2017 G.I.C.)| Onda viajera en una cuerda tensa ]]== | ==[[ Onda viajera en una cuerda tensa (Nov. 2017 G.I.C.)| Onda viajera en una cuerda tensa ]]== | ||
Una onda viajera en una cuerda tensa está descrita por la | Una onda viajera en una cuerda tensa está descrita por la | ||
última version al 10:42 23 ene 2018
1 Partícula en plano inclinado con dos muelles
Una masa m desliza sin rozamiento sobre un plano inclinado un ángulo β respecto a la horizontal. La barra está conectada a dos muelles ideales como se indica en la figura. Los muelles tienen constante elástica k y longitud natural nula. El muelle se ajusta de modo que k = mg / L. El ángulo β cumple

- Escribe la expresión que da la energía mecánica de la partícula para cualquier punto del plano.
- En el instante inicial la partícula está en el punto A y se le comunica una velocidad de módulo v0 dirigida hacia arriba. ¿Que valor mínimo debe tener v0 para que la partícula llegue hasta el punto B?
- Repite el cálculo del apartado anterior si hay un rozamiento entre la partícula y el plano con coeficiente de rozamiento dinámico μ = 0.5.
2 Onda viajera en una cuerda tensa
Una onda viajera en una cuerda tensa está descrita por la expresión
y(x,t) = 2.00cos(12.57x − 638t),
donde y se mide en cm, x en m y t en s. La densidad lineal de masa de la
cuerda es 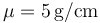 .
.
- ¿Cuanto valen la longitud de onda y el período de la onda?
- ¿Cuanto vale la tensión de la cuerda?
- ¿Cual es el máximo valor de la velocidad de un punto de la cuerda?
- ¿Cual es la potencia que transmite la onda?