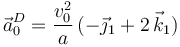Entrar Página Discusión Historial Go to the site toolbox

F1 GIA SPC 2015, Esfera con movimiento en función del tiempo

De Laplace

(Diferencias entre revisiones)
(Página creada con '== Enunciado == right Una esfera de radio <math>a </math>, se mueve en contacto con un plano <math>\Pi=OX_1Y_1 </math>. El mo…')
(→Rotación pura instantánea)
 
(Una edición intermedia no se muestra.)
Línea 35: Línea 35:
</math>
</math>
</center>
</center>
-
En la segunda solución, también se tiene <math>\vec{t_2}=\vec{0} </math>, por lo que respuesta correcta es la primera
+
En la segunda solución, también se tiene <math>\vec{\omega}=\vec{0} </math>, por lo que respuesta correcta es la primera
<center>
<center>
<math>
<math>
Línea 49: Línea 49:
</math>
</math>
</center>
</center>
 +
Haciendo el producto vectorial llegamos a la expresión
 +
<center>
 +
<math>
 +
\vec{\omega}\times\vec{v}^C = \dfrac{v_0^3}{a}\,\left(t-\dfrac{v_0}{a}t^2\right)\,\vec{k}_1
 +
</math>
 +
</center>
 +
Este vector se anula para dos instantes de tiempo
 +
<center>
 +
<math>
 +
t_1 = 0, \qquad t_2 = \dfrac{a}{v_0}
 +
</math>
 +
</center>
 +
Igual que antes, para <math>t=t_2 </math> tenemos <math>\vec{\omega}(t_2)=\vec{0} </math>. En este caso no hay velocidad mínima del campo de velocidades, pues no existe el eje instantáneo. La solución correcta es
 +
<center>
 +
<math>
 +
t=t_1=0
 +
</math>
 +
</center>
 +
 +
=== Aceleración del punto <math>D </math> ===
 +
Derivamos la reducción cinemática en <math>D </math>. Tenemos
 +
<center>
 +
<math>
 +
\vec{\alpha} = \dfrac{\mathrm{d}\vec{\omega}}{\mathrm{d}t}
 +
=
 +
-\dfrac{v_0^2}{a^2}\,(\vec{\imath}_1 + \vec{\jmath}_1)
 +
</math>
 +
</center>
 +
Derivando la velocidad tenemos
 +
<center>
 +
<math>
 +
\vec{a}^C = \dfrac{\mathrm{d}\vec{v}^C}{\mathrm{d}t}
 +
=
 +
-\dfrac{v_0^2}{a}\,\vec{\imath}_1
 +
</math>
 +
</center>
 +
Evaluamos la reducción cinemática y su derivada en el instante <math>t=2a/v_0 </math>. Indicamos con el subíndice 0 los valores particulares en este instante de tiempo
 +
<center>
 +
<math>
 +
\begin{array}{l}
 +
\vec{\omega}_0 = -\dfrac{v_0}{a}\,(\vec{\imath}_1+\vec{\jmath}_1)
 +
\\
 +
\vec{v}^C_0 = v_0\,(-\vec{\imath}_1 + \vec{\jmath}_1)
 +
\\
 +
\vec{\alpha}_0 = -\dfrac{v_0^2}{a^2}\,(\vec{\imath}_1+\vec{\jmath}_1)
 +
\\
 +
\vec{a}^C_0 = -\dfrac{v_0^2}{a}\,\vec{\imath}_1
 +
\end{array}
 +
</math>
 +
</center>
 +
Los valores de <math>\vec{\alpha}_0 </math> y <math>\vec{a}^C_0 </math> son los mismos que hemos encontrado antes, pues la aceleración y la aceleración angular son vectores constantes
 +
 +
Usamos la ecuación del campo de aceleraciones para relacionar las aceleraciones en los puntos <math>C </math> y <math>D </math>.
 +
<center>
 +
<math>
 +
\vec{a}^D_0 = \vec{a}^C_0 + \vec{\alpha}_0\times\overrightarrow{CD} +
 +
\vec{\omega}_0\times(\vec{\omega}_0\times\overrightarrow{CD})
 +
</math>
 +
</center>
 +
Del dibujo vemos que el vector geométrico es
 +
<center>
 +
<math>
 +
\overrightarrow{CD} = -a\,\vec{k}_1
 +
</math>
 +
</center>
 +
Los vectores que aparecen son
 +
<center>
 +
<math>
 +
\vec{\alpha}_0\times\overrightarrow{CD} = \dfrac{v_0^2}{a}\,(\vec{\imath}_1-\vec{\jmath}_1)
 +
</math>
 +
</center>
 +
Por otro lado
 +
<center>
 +
<math>
 +
\vec{\omega}_0\times\overrightarrow{CD} = v_0\,(\vec{\imath}_1 - \vec{\jmath}_1)
 +
</math>
 +
</center>
 +
y
 +
<center>
 +
<math>
 +
\vec{\omega}_0\times(\vec{\omega}_0\times\overrightarrow{CD}) = \dfrac{2v_0^2}{a}\,\vec{k}_1
 +
</math>
 +
</center>
 +
Sumando los tres términos tenemos
 +
<center>
 +
<math>
 +
\vec{a}^D_0 = \dfrac{v_0^2}{a}\,(-\vec{\jmath}_1 + 2\,\vec{k}_1)
 +
</math>
 +
</center>
 +
 +
[[Categoría:Problemas de examen F1 GIA]]
 +
[[Categoría:Problemas de cinemática del sólido rígido]]

última version al 12:10 30 nov 2016

Contenido

1 Enunciado

Una esfera de radio a, se mueve en contacto con un plano Π = OX1Y1. El movimiento de la esfera queda completamente caracterizado, para todo instante de tiempo, por la reducción cinemática

\begin{array}{c} \vec{\omega}(t) = \dfrac{v_0}{a}\,\left(1-\dfrac{v_0}{a}t\right)\,\left(\vec{\imath}_1+\vec{\jmath}_1\right) \\ \\ \vec{v}^C(t) = v_0\left[\left(1-\dfrac{v_0}{a}t\right)\,\vec{\imath}_1 + \vec{\jmath}_1\right] \end{array}

  1. En qué instante(s) el movimiento de la esfera respecto del plano es una rotación pura instantánea?
  2. En qué instante la velocidad del centro C tiene módulo mínimo en el campo de velocidades de la esfera?
  3. Aceleración del punto de la esfera que ocupa la posición D de contacto con el plano, en el instante t0 = 2a / v0?
  4. Calcula la aceleración del punto de la esfera que ocupa la posición D de contacto con el plano, en el instante t0 = 2a / v0

2 Solución

2.1 Rotación pura instantánea

Para que el movimiento sea una rotación pura el invariante escalar debe ser cero y el vector rotación debe ser distinto de cero. El invariante escalar es

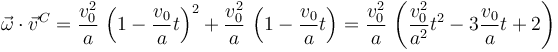
\vec{\omega}\cdot\vec{v}^C = \dfrac{v_0^2}{a}\,\left(1-\dfrac{v_0}{a}t\right)^2 + \dfrac{v_0^2}{a}\,\left(1-\dfrac{v_0}{a}t\right) = \dfrac{v_0^2}{a} \,\left(\dfrac{v_0^2}{a^2}t^2-3\dfrac{v_0}{a}t + 2\right)

Igualando a cero obtenemos dos posible soluciones

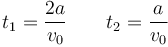
t_1=\dfrac{2a}{v_0}\qquad t_2=\dfrac{a}{v_0}

En la segunda solución, también se tiene 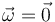\vec{\omega}=\vec{0} , por lo que respuesta correcta es la primera

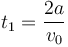
t_1 = \dfrac{2a}{v_0}

2.2 Velocidad con módulo mínimo en el campo de velocidades

Cuando esto se cumple, el punto C debe estar en el eje instantáneo del movimiento. Para ello, los vectores \vec{\omega} y \vec{v}^C deben ser paralelos, esto es

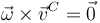
\vec{\omega}\times\vec{v}^C = \vec{0}

Haciendo el producto vectorial llegamos a la expresión

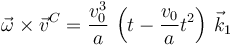
\vec{\omega}\times\vec{v}^C = \dfrac{v_0^3}{a}\,\left(t-\dfrac{v_0}{a}t^2\right)\,\vec{k}_1

Este vector se anula para dos instantes de tiempo

t_1 = 0, \qquad t_2 = \dfrac{a}{v_0}

Igual que antes, para t = t2 tenemos 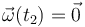\vec{\omega}(t_2)=\vec{0} . En este caso no hay velocidad mínima del campo de velocidades, pues no existe el eje instantáneo. La solución correcta es

t = t1 = 0

2.3 Aceleración del punto D

Derivamos la reducción cinemática en D. Tenemos

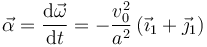
\vec{\alpha} = \dfrac{\mathrm{d}\vec{\omega}}{\mathrm{d}t} = -\dfrac{v_0^2}{a^2}\,(\vec{\imath}_1 + \vec{\jmath}_1)

Derivando la velocidad tenemos

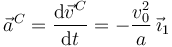
\vec{a}^C = \dfrac{\mathrm{d}\vec{v}^C}{\mathrm{d}t} = -\dfrac{v_0^2}{a}\,\vec{\imath}_1

Evaluamos la reducción cinemática y su derivada en el instante t = 2a / v0. Indicamos con el subíndice 0 los valores particulares en este instante de tiempo

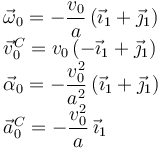
\begin{array}{l} \vec{\omega}_0 = -\dfrac{v_0}{a}\,(\vec{\imath}_1+\vec{\jmath}_1) \\ \vec{v}^C_0 = v_0\,(-\vec{\imath}_1 + \vec{\jmath}_1) \\ \vec{\alpha}_0 = -\dfrac{v_0^2}{a^2}\,(\vec{\imath}_1+\vec{\jmath}_1) \\ \vec{a}^C_0 = -\dfrac{v_0^2}{a}\,\vec{\imath}_1 \end{array}

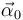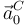Los valores de \vec{\alpha}_0 y \vec{a}^C_0 son los mismos que hemos encontrado antes, pues la aceleración y la aceleración angular son vectores constantes

Usamos la ecuación del campo de aceleraciones para relacionar las aceleraciones en los puntos C y D.

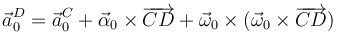
\vec{a}^D_0 = \vec{a}^C_0 + \vec{\alpha}_0\times\overrightarrow{CD} + \vec{\omega}_0\times(\vec{\omega}_0\times\overrightarrow{CD})

Del dibujo vemos que el vector geométrico es

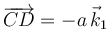
\overrightarrow{CD} = -a\,\vec{k}_1

Los vectores que aparecen son

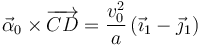
\vec{\alpha}_0\times\overrightarrow{CD} = \dfrac{v_0^2}{a}\,(\vec{\imath}_1-\vec{\jmath}_1)

Por otro lado

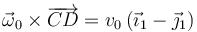
\vec{\omega}_0\times\overrightarrow{CD} = v_0\,(\vec{\imath}_1 - \vec{\jmath}_1)

y

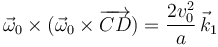
\vec{\omega}_0\times(\vec{\omega}_0\times\overrightarrow{CD}) = \dfrac{2v_0^2}{a}\,\vec{k}_1

Sumando los tres términos tenemos

\vec{a}^D_0 = \dfrac{v_0^2}{a}\,(-\vec{\jmath}_1 + 2\,\vec{k}_1)

Obtenido de "http://tesla.us.es/wiki/index.php/F1_GIA_SPC_2015,_Esfera_con_movimiento_en_funci%C3%B3n_del_tiempo"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 12:10, 30 nov 2016. - Esta página ha sido visitada 2.510 veces. - Aviso legal - Acerca de Laplace