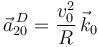Entrar Página Discusión Historial Go to the site toolbox

Disco contenido en plano rotante, Enero 2015 (F1 GIA)

De Laplace

(Diferencias entre revisiones)
(Página creada con '==Enunciado == right Un disco de radio <math>R </math> (sólido "2"), se mueve siempre contenido en el plano <math>O…')
Línea 22: Línea 22:
<center>
<center>
<math>
<math>
-
\vec{a}^{\,C}_{20} = \left.\dfrac{\mathrm{d}\vec{v}^{\,C}_{20}}{\mathrm{d}t}\right| = \vec{0}
+
\vec{a}^{\,C}_{20} = \left.\dfrac{\mathrm{d}\vec{v}^{\,C}_{20}}{\mathrm{d}t}\right|_0 = \vec{0}
</math>
</math>
</center>
</center>
-
El plano realiza una rotación de eje permanente <math>OZ_0 </math>, con velocidad angular constante. La velocidad del movimiento {01} de cualquier punto del eje es nula. Por tanto
+
El movimiento {20} es una rotación instantánea, con el eje perpendicular al plano del disco, por tanto
<center>
<center>
<math>
<math>
-
\vec{\omega}_{01} = \Omega\,\vec{k}_0\qquad \vec{v}^{\,O_1}_{01} = \vec{0}
+
\vec{\omega}_{20} = \omega_{20}\,\vec{\jmath}_0
 +
</math>
 +
</center>
 +
Usamos el teorema de Chasles para calcular <math>\omega_{20} </math>
 +
<center>
 +
<math>
 +
\left.
 +
\begin{array}{l}
 +
\vec{v}^{\,C}_{20} = -v_0\,\vec{\imath}_0
 +
\\
 +
\\
 +
\vec{v}^{\,C}_{20} = \vec{v}^{\,D}_{20} + \vec{\omega}_{20}\times\overrightarrow{DC}
 +
=
 +
(\omega_{20}\,\vec{\jmath})\times(R\,\vec{k}) =
 +
\omega_{20}R\,\vec{\imath}_0
 +
\end{array}
 +
\right|
 +
\Longrightarrow
 +
\vec{\omega}_{20} = -\dfrac{v_0}{R}\,\vec{\jmath}_0
 +
</math>
 +
</center>
 +
El plano realiza una rotación de eje permanente <math>OZ_0 </math>, con velocidad angular constante. La velocidad del movimiento {01} de cualquier punto del eje es nula en todo instante. Por tanto
 +
<center>
 +
<math>
 +
\vec{\omega}_{01} = \Omega\,\vec{k}_0\qquad \vec{v}^{\,O_1}_{01} = \vec{0},
 +
\qquad \vec{a}^{\,O_1}_{01} = \left.\dfrac{\mathrm{d}\vec{v}^{\,O_1}_{01}}{\mathrm{d}t}\right|_1 = \vec{0}
</math>
</math>
</center>
</center>
Línea 37: Línea 62:
<math>
<math>
\vec{a}^{\,D}_{21} = \vec{a}^{\,D}_{20} + \vec{a}^{\,D}_{01} + 2\,\vec{\omega}_{01}\times\vec{v}^{\,D}_{20}
\vec{a}^{\,D}_{21} = \vec{a}^{\,D}_{20} + \vec{a}^{\,D}_{01} + 2\,\vec{\omega}_{01}\times\vec{v}^{\,D}_{20}
 +
</math>
 +
</center>
 +
Examinemos cada uno de los tres términos
 +
<center>
 +
<math>
 +
\vec{a}^{\,D}_{20} = \vec{a}^{\,C}_{20} + \vec{\alpha}_{20}\times\overrightarrow{CD} +
 +
\vec{\omega}_{20}\times(\vec{\omega}_{20}\times\overrightarrow{CD})
 +
</math>
 +
</center>
 +
El primer sumando es cero. El segundo también, pues
 +
<center>
 +
<math>
 +
\vec{\alpha}_{20} = \left.\dfrac{\mathrm{d}\vec{\omega}_{20}}{\mathrm{d}t}\right|_0 = \vec{0}
 +
</math>
 +
</center>
 +
Sólo queda el tercero, y tenemos
 +
<center>
 +
<math>
 +
\vec{\omega}_{20}\times(\vec{\omega}_{20}\times\overrightarrow{CD})
 +
=
 +
\dfrac{v_0^2}{R}\,\vec{k}_0
 +
</math>
 +
</center>
 +
Entonces
 +
<center>
 +
<math>
 +
\vec{a}^{\,D}_{20} = \dfrac{v_0^2}{R}\,\vec{k}_0
</math>
</math>
</center>
</center>

Revisión de 16:23 30 ene 2015

Contenido

1 Enunciado

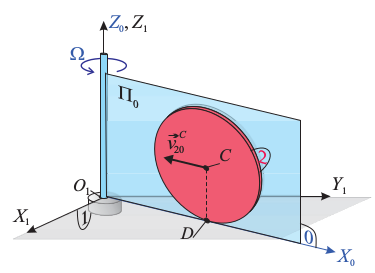
Un disco de radio R (sólido "2"), se mueve siempre contenido en el plano OX0Z0 (sólido "0"), rodando sin deslizar sobre el eje OX0; además, su centro C se desplaza en dicho plano dirigiéndose hacia el eje OZ0 con velocidad constante v0. El plano Π0 se mantiene siempre vertical y perpendicular al plano fijo Π1, pero girando en sentido antihorario alrededor del eje OZ0 = OZ1, con velocidad angular constante de valor Ω. Obtenga la expresión de la aceleración, medida desde el sólido "1", del punto del disco que ocupa la posición D de contacto con el plano Π1, en el instante en que el centro C se encuentra a una distancia d del eje OZ0,1. ¿Cuáles son las componentes intrínsecas de dicha aceleración?

2 Solución

El enunciado nos pide que calculemos 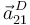\vec{a}^{\,D}_{21} . Hay varias formas de hacerlo. Vamos a ver dos.

3 Información cinemática del enunciado

El disco rueda sin deslizar sobre el eje OX0, por tanto

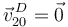
\vec{v}^{\,D}_{20} = \vec{0}

El centro del disco se mueve con velocidad

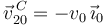
\vec{v}^{\,C}_{20} = -v_0\,\vec{\imath}_0

Además, este punto tiene siempre la misma velocidad en el movimiento {20}, porque es el centro del disco. Entonces

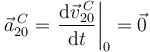
\vec{a}^{\,C}_{20} = \left.\dfrac{\mathrm{d}\vec{v}^{\,C}_{20}}{\mathrm{d}t}\right|_0 = \vec{0}

El movimiento {20} es una rotación instantánea, con el eje perpendicular al plano del disco, por tanto

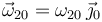
\vec{\omega}_{20} = \omega_{20}\,\vec{\jmath}_0

Usamos el teorema de Chasles para calcular ω20

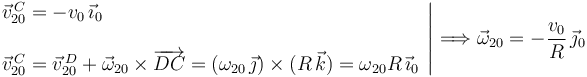
\left. \begin{array}{l} \vec{v}^{\,C}_{20} = -v_0\,\vec{\imath}_0 \\ \\ \vec{v}^{\,C}_{20} = \vec{v}^{\,D}_{20} + \vec{\omega}_{20}\times\overrightarrow{DC} = (\omega_{20}\,\vec{\jmath})\times(R\,\vec{k}) = \omega_{20}R\,\vec{\imath}_0 \end{array} \right| \Longrightarrow \vec{\omega}_{20} = -\dfrac{v_0}{R}\,\vec{\jmath}_0

El plano realiza una rotación de eje permanente OZ0, con velocidad angular constante. La velocidad del movimiento {01} de cualquier punto del eje es nula en todo instante. Por tanto

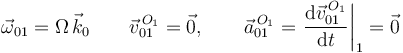
\vec{\omega}_{01} = \Omega\,\vec{k}_0\qquad \vec{v}^{\,O_1}_{01} = \vec{0}, \qquad \vec{a}^{\,O_1}_{01} = \left.\dfrac{\mathrm{d}\vec{v}^{\,O_1}_{01}}{\mathrm{d}t}\right|_1 = \vec{0}

3.1 Resolución con composición de movimientos

Usando el teorema de Coriolis podemos calcular 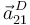\vec{a}^{\,D}_{21} como

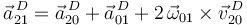
\vec{a}^{\,D}_{21} = \vec{a}^{\,D}_{20} + \vec{a}^{\,D}_{01} + 2\,\vec{\omega}_{01}\times\vec{v}^{\,D}_{20}

Examinemos cada uno de los tres términos

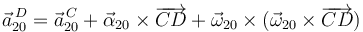
\vec{a}^{\,D}_{20} = \vec{a}^{\,C}_{20} + \vec{\alpha}_{20}\times\overrightarrow{CD} + \vec{\omega}_{20}\times(\vec{\omega}_{20}\times\overrightarrow{CD})

El primer sumando es cero. El segundo también, pues

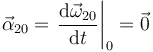
\vec{\alpha}_{20} = \left.\dfrac{\mathrm{d}\vec{\omega}_{20}}{\mathrm{d}t}\right|_0 = \vec{0}

Sólo queda el tercero, y tenemos

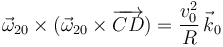
\vec{\omega}_{20}\times(\vec{\omega}_{20}\times\overrightarrow{CD}) = \dfrac{v_0^2}{R}\,\vec{k}_0

Entonces

\vec{a}^{\,D}_{20} = \dfrac{v_0^2}{R}\,\vec{k}_0

Obtenido de "http://tesla.us.es/wiki/index.php/Disco_contenido_en_plano_rotante,_Enero_2015_(F1_GIA)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace