Problemas de introducción a la física (GIE)
De Laplace
(→Ejemplo de estimación de longitudes y volúmenes) |
(→Estimación del radio terrestre) |
||
| Línea 153: | Línea 153: | ||
==[[Estimación del radio terrestre]]== | ==[[Estimación del radio terrestre]]== | ||
| - | De un lago se sabe que tiene 6 | + | De un lago se sabe que tiene 6 km de anchura. Desde un punto de una orilla no se ve la otra, pero se comprueba que subiendo al balcón del primer piso, sí se ve. Estime el radio de la Tierra. |
==[[Ejemplo de estimación de longitudes y volúmenes]]== | ==[[Ejemplo de estimación de longitudes y volúmenes]]== | ||
Revisión de 22:52 22 sep 2011
Contenido |
1 Ejemplos de valores numéricos
Las siguientes cantidades representan aproximadamente los valores de las magnitudes de la tabla, expresadas en las unidades fundamentales del SI o productos de ellas. Indique cuál le corresponde a cada una, indicando sus unidades.
| 1 | Peso de una persona | 2 | Densidad de masa del agua | 3 | Aceleración de la Tierra alrededor del Sol |
| 4 | Masa de la Tierra | 5 | Diámetro de un glóbulo rojo | 6 | Distancia Tierra-Sol |
| 7 | Altura a la que se encuentra la Estación Espacial Internacional | 8 | Radio de un átomo | 9 | Densidad del oro |
| 10 | Diámetro de una pelota de golf | 11 | Espesor de un folio | 12 | Aceleración de la gravedad |
| 13 | Volumen aproximado de oro en la Tierra | 14 | Velocidad de Usain Bolt en los 100m | 15 | Masa de un m³ de agua |
| 16 | Duración de un año | 17 | Velocidad de una bacteria | 18 | Periodo de la corriente alterna doméstica |
| 19 | Masa del electrón | 20 | Velocidad de la luz | 21 | Circunferencia terrestre |
| A | 10−30 | B | 10−10 | C | 6×10−6 |
| D | 5×10−5 | E | 6×10−3 | F | 2×10−2 |
| G | 5×10−2 | H | 10−1 | I | 10 |
| J | 10 | K | 8× 102 | L | 103 |
| M | 103 | N | 103 | O | 6×104 |
| P | 2×104 | Q | 5×105 | R | 3×107 |
| S | 4×107 | T | 3× 108 | U | 1.5×1011 |
2 Ejemplos de cálculo de dimensiones
A partir de las relaciones definitorias
| Velocidad | Cantidad de movimiento | Aceleración | Fuerza |
|---|---|---|---|
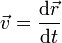
| 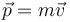
| 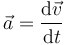
| 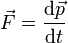
|
| Trabajo | Potencia | Momento cinético | Momento de una fuerza |
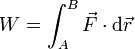
| 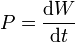
| 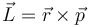
| 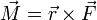
|
determine las ecuaciones dimensionales de estas magnitudes, así como sus unidades en el Sistema Internacional (SI) en función de las unidades fundamentales de este sistema.
3 Dependencias del periodo de un péndulo
Un péndulo simple es una masa m suspendida de un hilo ideal (sin masa), que tiene una longitud l. La masa está sometida a la aceleración de la gravedad, g. El péndulo llega a separarse de la vertical un cierto ángulo θ0.
Si duplicamos la longitud del péndulo, ¿cómo cambiará su periodo de oscilación? ¿Y si nos llevamos el péndulo a la Luna, donde la gravedad es 1/6 de la terrestre?
4 Ejemplos de estimaciones numéricas
Estime las siguientes cantidades:
- El número de latidos del corazón de una persona a lo largo de su vida.
- Las bolas que hay en la máquina de la figura.
- La velocidad de reproducción en bits/s de un CD de música.

5 Estimación del radio terrestre
De un lago se sabe que tiene 6 km de anchura. Desde un punto de una orilla no se ve la otra, pero se comprueba que subiendo al balcón del primer piso, sí se ve. Estime el radio de la Tierra.
6 Ejemplo de estimación de longitudes y volúmenes
Se tiene un bloque de aluminio de forma cúbica cuya masa es aproximadamente 2.5 kg. Estime el valor de la arista del cubo, así como su superficie lateral. Si se sabe que la incertidumbre de la medida de la masa es de 100 g, ¿entre qué valores se hallarán la arista y el área lateral?
¿Y si en vez de aluminio fuera oro?





