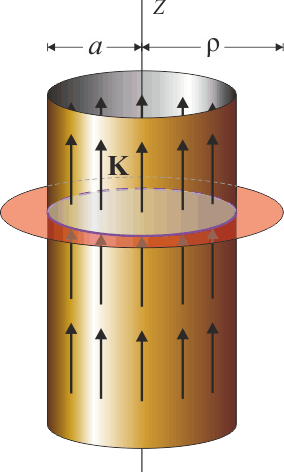
Campo de un tubo cilíndrico

De Laplace

(Diferencias entre revisiones)

última version al 22:30 31 may 2011

Contenido

1 Enunciado
2 Introducción
3 En forma integral
4 En forma diferencial

1 Enunciado

Sobre un cilindro de radio $a$ y longitud infinita fluye una corriente superficial de densidad uniforme 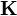$\mathbf{K}$ . Halle el campo magnético en todos los puntos del espacio.

2 Introducción

Aunque el enunciado no dice explícitamente hacia dónde se dirige la corriente, si esta es uniforme, no puede ser otra que

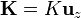
$\mathbf{K}=K\mathbf{u}_{z}\,$

Si supusiéramos, por ejemplo, una corriente 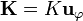$\mathbf{K}=K\mathbf{u}_{\varphi}$ no sería uniforme, pues 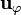$\mathbf{u}_{\varphi}$ depende de la posición.

El problema puede resolverse empleando las ecuaciones de la magnetostática en forma diferencial y en forma integral.

3 En forma integral

El cálculo del campo en forma integral es muy parecido al del caso de un hilo rectilíneo o de un cable grueso, por lo que simplemente adaptaremos la solución del caso de un hilo al caso que nos ocupa:

Por comodidad, emplearemos coordenadas cilíndricas, situando el eje Z coincidente con el del cilindro. El campo magnético producido por el hilo tiene tres componentes, dependiente cada una, en principio, de las tres coordenadas

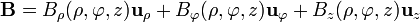
$\mathbf{B} = B_\rho(\rho,\varphi,z)\mathbf{u}_{\rho} + B_\varphi(\rho,\varphi,z)\mathbf{u}_{\varphi} + B_z(\rho,\varphi,z)\mathbf{u}_{z}$

Sin embargo, este sistema posee simetría traslacional a lo largo del eje Z (esto es, que si nos desplazamos paralelamente al eje no percibimos ningún cambio), por lo que ninguna de las componentes depende de esta coordenada

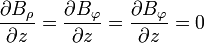
$\frac{\partial{}B_\rho}{\partial z} = \frac{\partial{}B_\varphi}{\partial z} = \frac{\partial{}B_\varphi}{\partial z} = 0$

Al mismo tiempo, el sistema también posee simetría rotacional alrededor del mismo eje (es decir, que un giro alrededor del eje, manteniendo la distancia constante, tampoco modifica nuestra visión del sistema). Por ello, las componentes son independientes de la coordenada $\varphi$ , que es la que se modifica al efectuar una rotación.

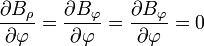
$\frac{\partial{}B_\rho}{\partial \varphi} = \frac{\partial{}B_\varphi}{\partial \varphi} = \frac{\partial{}B_\varphi}{\partial \varphi} = 0$

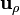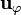Nótese que, aunque ninguna componente depende de $\varphi$ , el campo sí lo hace, a través de los vectores de la base $\mathbf{u}_{\rho}$ y $\mathbf{u}_{\varphi}$ .

Con estas dos simplificaciones, el campo nos queda en la forma

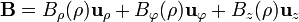
$\mathbf{B} = B_\rho(\rho)\mathbf{u}_{\rho} + B_\varphi(\rho)\mathbf{u}_{\varphi} + B_z(\rho)\mathbf{u}_{z}$

El siguiente paso consiste en demostrar que la componente $B z$ es nula. Para ello, lo más sencillo es recurrir directamente a la ley de Biot y Savart

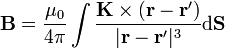
$\mathbf{B}=\frac{\mu_0}{4\pi}\int \frac{\mathbf{K}\times(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}\mathrm{d}\mathbf{S}$

Lo que nos interesa aquí es observar que, debido al producto vectorial, el integrando es perpendicular tanto a 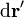$\mathrm{d}\mathbf{r}'$ como a 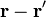$\mathbf{r}-\mathbf{r}'$ . Ahora bien, por tratarse de un hilo rectilíneo,

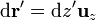
$\mathrm{d}\mathbf{r}' = \mathrm{d}z'\mathbf{u}_{z}$

esto es, el diferencial va siempre en la misma dirección y sentido, por lo que el integrando es siempre ortogonal a esta dirección y el campo total, por tanto, también lo es

$B_z = 0\,$

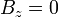
Este resultado es un caso particular de una propiedad más general del campo magnético, de ser ortogonal a la corriente que lo produce.

A continuación, veremos que también la componente radial es nula. Para ello, emplearemos la ley de Gauss para el campo magnético

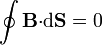
$\oint \mathbf{B}{\cdot}\mathrm{d}\mathbf{S}=0$

aplicada a un volumen cilíndrico concéntrico con el tubo de corriente. Este cilindro lo tomaremos de radio $ρ$ y altura $h$ . El flujo a través de las caras de este cilindro se compone de tres términos: las dos bases, $S 1$ y $S 2$ , y la superficie lateral, $S L$

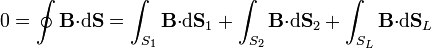
$0 = \oint\mathbf{B}{\cdot}\mathrm{d}\mathbf{S} = \int_{S_1}\mathbf{B}{\cdot}\mathrm{d}\mathbf{S}_1 + \int_{S_2}\mathbf{B}{\cdot}\mathrm{d}\mathbf{S}_2 + \int_{S_L} \mathbf{B}{\cdot}\mathrm{d}\mathbf{S}_L$

En las dos bases, el vector superficie va en la dirección de 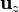$\mathbf{u}_{z}$ , por lo que el producto escalar por el campo magnético se anula

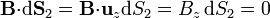
$\mathbf{B}{\cdot}\mathrm{d}\mathbf{S}_2 = \mathbf{B}{\cdot}\mathbf{u}_{z}\mathrm{d}S_2 = B_z\,\mathrm{d}S_2 = 0$

Queda la integral sobre la cara lateral, que es una superficie $ρ = cte.$ , por lo que el diferencial de superficie vale

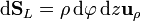
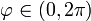
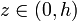
$\mathrm{d}\mathbf{S}_L = \rho \,\mathrm{d}\varphi\,\mathrm{d}z\mathbf{u}_{\rho}$ $\varphi\in(0,2\pi)$ $z\in(0,h)$

y las componentes de $\mathbf{B}$ son constantes en esta superficie, por lo que

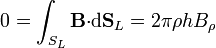
$0 = \int_{S_L}\mathbf{B}{\cdot}\mathrm{d}\mathbf{S}_L = 2\pi\rho h B_\rho$ $\Rightarrow$

B ρ = 0

Este resultado puede entenderse gráficamente. Al ser el flujo del campo magnético siempre nulo, el campo no puede manar de la línea, ni ir hacia ella, por lo que la componente radial debe anularse.

Queda solamente hallar la componente acimutal, 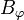$B_\varphi$ . Para ello, aplicamos la ley de Ampère en forma integral

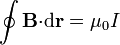
$\oint\mathbf{B}{\cdot}\mathrm{d}\mathbf{r} = \mu_0I$

a un contorno circular situado en un plano circular ortogonal al tubo de corriente y centrado en su eje. Para este contorno el diferencial de longitud vale

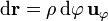
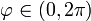
$\mathrm{d}\mathbf{r} = \rho\,\mathrm{d}\varphi\,\mathbf{u}_{\varphi}$ $\varphi\in(0,2\pi)$

y la circulación

$\oint \mathbf{B}{\cdot}\mathrm{d}\mathbf{r} = 2\pi\rho B_\varphi = \mu_0 I(\rho)$

La corriente abarcada depende si el radio de la curva de integración es menor o mayor que el del tubo.

Interior del tubo: Si $ρ < a$ la circunferencia no abarca ninguna corriente, que fluye completamente por exterior, por lo que

$I(\rho) = 0 \qquad (\rho< a)$

y por tanto el campo es nulo en el interior del tubo

$\mathbf{B}=\mathbf{0}\qquad (\rho < a)$

Exterior del tubo: Si $ρ > a$ la circunferencia abarca toda la corriente que fluye por el tubo. La corriente que atraviesa un disco apoyado sobre la circunferencia es igual a

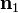$I = \int \mathbf{K}\cdot\mathbf{n}_1\mathrm{d}l$

siendo $\mathbf{n}_1$ un vector unitario tangente al cubo y normal al disco. Este vector es $\mathbf{u}_z$ . Por su parte el diferencial de camino sobre esta sección del tubo es

$\mathrm{d}l = a\,\mathrm{d}\varphi$

así que queda

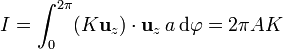
$I = \int_0^{2\pi}(K\mathbf{u}_z)\cdot\mathbf{u}_z\,a\,\mathrm{d}\varphi = 2\pi A K$

lo que nos da finalmente para el campo magnético en el exterior

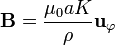
$\mathbf{B} = \frac{\mu_0aK}{\rho}\mathbf{u}_{\varphi}$

Reuniendo ambos resultados

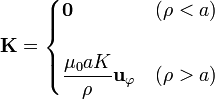
$\mathbf{K}=\begin{cases} \mathbf{0} & (\rho < a)\\ & \\ \displaystyle\frac{\mu_0aK}{\rho}\mathbf{u}_{\varphi} & (\rho>a)\end{cases}$

Las líneas de campo magnético describen circunferencias en torno al tubo según la regla de la mano derecha. El módulo del campo es nulo en el interior y decae como la inversa de la distancia al eje, esto es, como si toda la corriente estuviera concentrada en el eje del tubo..

4 En forma diferencial

En forma diferencial debemos resolver las ecuaciones de la magnetostática

$\begin{array}{rcl} \nabla\cdot\mathbf{B} & = & 0 \\ && \\ \nabla\times\mathbf{B} & = & \mu_0\mathbf{J}=\mathbf{0} \end{array}$

junto con las correspondientes condiciones de salto en la superficie del cilindro:

$\begin{array}{rcl} \mathbf{n}\cdot[\mathbf{B}] & = & 0 \\ && \\ \mathbf{n}\times[\mathbf{B}] & = & \mu_0\mathbf{K} \end{array}$

Además, debemos tener en cuenta que el campo magnético sólo se puede hacer infinito en puntos donde haya distribuciones de corriente lineales, nunca donde no haya corriente. También que en puntos alejados del cilindro el campo debe anularse.

Tenemos que, como en el caso del cable grueso, existe simetría traslacional y rotacional. Por ello, ninguna de las tres componentes depende de $z$ ni de $\varphi$ .

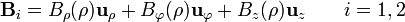
$\mathbf{B}_i = B_\rho(\rho)\mathbf{u}_\rho+B_\varphi(\rho)\mathbf{u}_\varphi+B_z(\rho)\mathbf{u}_z\qquad i = 1,2$

donde denominamos región 1 al interior del tubo y región 2 al exterior.

Aplicando la ley de Gauss para el campo magnético resulta

$0 = \nabla\cdot\mathbf{B} = \frac{1}{\rho}\frac{\mathrm{d}\ }{\mathrm{d}\rho}\left(\rho B_\rho\right)\quad\Rightarrow\quad B_\rho = \frac{k_i}{\rho}$

siendo $k i$ dos constantes, una para el interior del tubo y otra para el exterior

Ahora bien, puesto que el campo no puede tender a 0 en $ρ = 0$ , ya que el campo no puede diverger donde no hay corrientes, resulta que

$k_1 = 0\,$

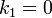
y aplicando ahora la condición de salto para la componente normal

$0 = \mathbf{n}\cdot[\mathbf{B}] = \mathbf{u}_\rho\cdot\left(\mathbf{B}_2(a^+)-\mathbf{B}_1(a^-)\right) = \frac{k_2}{a}-0\quad\Rightarrow\quad k_2 = 0$

y por tanto, como consecuencia de la ley de Gauss para el campo magnético, la componente radial es nula en todo el espacio.

$B_\rho=0\,$

Aplicando ahora la ley de Ampère en cada región tenemos

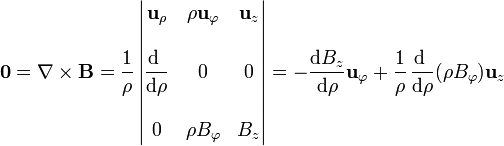
$\mathbf{0}=\nabla\times\mathbf{B}=\frac{1}{\rho}\left|\begin{matrix}\mathbf{u}_\rho & \rho\mathbf{u}_\varphi & \mathbf{u}_z \\ & & \\ \displaystyle\frac{\mathrm{d}\ }{\mathrm{d}\rho} & 0 & 0 \\ & & \\ 0 & \rho B_\varphi & B_z\end{matrix}\right| = -\frac{\mathrm{d}B_z}{\mathrm{d}\rho}\mathbf{u}_\varphi + \frac{1}{\rho}\,\frac{\mathrm{d}\ }{\mathrm{d}\rho}(\rho B_\varphi)\mathbf{u}_z$

Un vector es nulo cuando son nulas cada una de sus componentes. Por ello, las componentes en el interior y el exterior pueden escribirse como

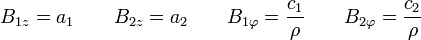
$B_{1z}=a_1\qquad B_{2z}=a_2\qquad B_{1\varphi}=\frac{c_1}{\rho}\qquad B_{2\varphi}=\frac{c_2}{\rho}$

La condición de que el campo no sea singular en el eje significa

$c_1=0\,$

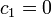
mientras que la anulación del campo en el infinito supone

$a_2=0\,$

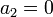
Las otras dos constantes se obtienen de la condición de salto, que en este caso es

$\mathbf{n}\times[\mathbf{B}]=a_1\mathbf{u}_{\varphi}+\frac{k_2}{R}\mathbf{u}_{z}=\mu_0\mathbf{K}=\mu_0 K\mathbf{u}_{z} \quad\Rightarrow\quad a_1=0\qquad k_2=\mu_0 K a$

con lo que el resultado final es que el campo se anula en el interior

$\mathbf{B}_1=0\,$

y en el exterior decae como la inversa de la distancia al eje

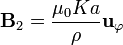
$\mathbf{B}_2=\frac{\mu_0 K a}{\rho}\mathbf{u}_{\varphi}$

Este campo exterior es idéntico al de un hilo de corriente cuya intensidad es

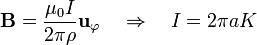
$\mathbf{B}=\frac{\mu_0I}{2\pi\rho}\mathbf{u}_{\varphi}\quad\Rightarrow\quad I=2\pi a K$

Esta corriente es justamente la cantidad total que fluye a través de una sección del tubo de corriente. Resulta entonces que el campo debido a un tubo hueco por el cual circula una corriente longitudinal, es nulo en el exterior y en el interior es el mismo que habría si toda la corriente circulara por el centro del tubo.

@@ Línea 12: / Línea 12: @@
 ==En forma integral==
+El cálculo del campo en forma integral es muy parecido al del caso de un hilo rectilíneo o de un cable grueso, por lo que simplemente adaptaremos la solución del caso de un hilo al caso que nos ocupa:
+Por comodidad, emplearemos coordenadas cilíndricas, situando el eje Z coincidente con el del cilindro. El campo magnético producido por el hilo tiene tres componentes, dependiente cada una, en principio, de las tres coordenadas
+<center><math>\mathbf{B} = B_\rho(\rho,\varphi,z)\mathbf{u}_{\rho} + B_\varphi(\rho,\varphi,z)\mathbf{u}_{\varphi} +
+ B_z(\rho,\varphi,z)\mathbf{u}_{z}</math></center>
+Sin embargo, este sistema posee ''[[Elección de ejes. Simetría|simetría traslacional]]'' a lo largo del eje Z (esto es, que si nos desplazamos paralelamente al eje no percibimos ningún cambio), por lo que ninguna de las componentes depende de esta coordenada
+<center><math>\frac{\partial{}B_\rho}{\partial z} = \frac{\partial{}B_\varphi}{\partial z} = \frac{\partial{}B_\varphi}{\partial z}  = 0</math></center>
+Al mismo tiempo, el sistema también posee [[Elección de ejes. Simetría|simetría rotacional]] alrededor del mismo eje (es decir, que un giro alrededor del eje, manteniendo la distancia constante, tampoco modifica nuestra visión del sistema). Por ello, las componentes son independientes de la coordenada <math>\varphi</math>, que es la que se modifica al efectuar una rotación.
+<center><math>\frac{\partial{}B_\rho}{\partial \varphi} = \frac{\partial{}B_\varphi}{\partial \varphi} = \frac{\partial{}B_\varphi}{\partial \varphi}  = 0</math></center>
+Nótese que, aunque ninguna componente depende de <math>\varphi</math>, el campo sí lo hace, a través de los vectores de la base <math>\mathbf{u}_{\rho}</math> y <math>\mathbf{u}_{\varphi}</math>.
+Con estas dos simplificaciones, el campo nos queda en la forma
+<center><math>\mathbf{B} = B_\rho(\rho)\mathbf{u}_{\rho} + B_\varphi(\rho)\mathbf{u}_{\varphi} +  B_z(\rho)\mathbf{u}_{z}</math></center>
+El siguiente paso consiste en demostrar que la componente <math>B_z</math> es nula. Para ello, lo más sencillo es recurrir directamente a la [[ley de Biot y Savart]]
+<center><math>\mathbf{B}=\frac{\mu_0}{4\pi}\int \frac{\mathbf{K}\times(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}\mathrm{d}\mathbf{S}</math></center>
+Lo que nos interesa aquí es observar que, debido al producto vectorial, el integrando es perpendicular tanto a <math>\mathrm{d}\mathbf{r}'</math> como a <math>\mathbf{r}-\mathbf{r}'</math>. Ahora bien, por tratarse de un hilo rectilíneo,
+<center><math>\mathrm{d}\mathbf{r}' = \mathrm{d}z'\mathbf{u}_{z}</math></center>
+esto es, el diferencial va siempre en la misma dirección y sentido, por lo que el integrando es siempre ortogonal a esta dirección y el campo total, por tanto, también lo es
+<center><math>B_z = 0\,</math></center>
+Este resultado es un caso particular de una propiedad más general del campo magnético, de ser ortogonal a la corriente que lo produce.
+A continuación, veremos que también la componente radial es nula. Para ello, emplearemos la [[ley de Gauss para el campo magnético]]
+<center><math>\oint \mathbf{B}{\cdot}\mathrm{d}\mathbf{S}=0</math></center>
+[[Imagen:gaussBtubo.png|left]]
+aplicada a un volumen cilíndrico concéntrico con el tubo de corriente. Este cilindro lo tomaremos de radio <math>\rho</math> y altura <math>h</math>. El flujo a través de las caras de este cilindro se compone de tres términos: las dos bases, <math>S_1</math> y <math>S_2</math>, y la superficie lateral, <math>S_L</math>
+<center><math>0 = \oint\mathbf{B}{\cdot}\mathrm{d}\mathbf{S} = \int_{S_1}\mathbf{B}{\cdot}\mathrm{d}\mathbf{S}_1 + \int_{S_2}\mathbf{B}{\cdot}\mathrm{d}\mathbf{S}_2 + \int_{S_L} \mathbf{B}{\cdot}\mathrm{d}\mathbf{S}_L</math></center>
+En las dos bases, el vector superficie va en la dirección de <math>\mathbf{u}_{z}</math>, por lo que el producto escalar por el campo magnético se anula
+<center><math>\mathbf{B}{\cdot}\mathrm{d}\mathbf{S}_2 = \mathbf{B}{\cdot}\mathbf{u}_{z}\mathrm{d}S_2 = B_z\,\mathrm{d}S_2 = 0</math></center>
+Queda la integral sobre la cara lateral, que es una superficie <math>\rho=\mathrm{cte.}</math>, por lo que el diferencial de superficie vale
+<center><math>\mathrm{d}\mathbf{S}_L = \rho \,\mathrm{d}\varphi\,\mathrm{d}z\mathbf{u}_{\rho}</math>{{qquad}}{{qquad}}<math>\varphi\in(0,2\pi)</math>{{qquad}} <math>z\in(0,h)</math></center>
+y las componentes de <math>\mathbf{B}</math> son constantes en esta superficie, por lo que
+<center><math>0 = \int_{S_L}\mathbf{B}{\cdot}\mathrm{d}\mathbf{S}_L = 2\pi\rho h B_\rho</math>{{tose}}<math>B_\rho=0</math></center>
+Este resultado puede entenderse gráficamente. Al ser el flujo del campo magnético siempre nulo, el campo no puede manar de la línea, ni ir hacia ella, por lo que la componente radial debe anularse.
+Queda solamente hallar la componente acimutal, <math>B_\varphi</math>. Para ello, aplicamos la [[ley de Ampère]] en forma integral
+<center><math>\oint\mathbf{B}{\cdot}\mathrm{d}\mathbf{r} = \mu_0I</math></center>
+[[Imagen:ampereBtubo.png|right]]
+a un contorno circular situado en un plano circular ortogonal al tubo de corriente y centrado en su eje. Para este contorno el diferencial de longitud vale
+<center><math>\mathrm{d}\mathbf{r} = \rho\,\mathrm{d}\varphi\,\mathbf{u}_{\varphi}</math>{{qquad}}<math>\varphi\in(0,2\pi)</math></center>
+y la circulación
+<center><math>\oint \mathbf{B}{\cdot}\mathrm{d}\mathbf{r} = 2\pi\rho B_\varphi = \mu_0 I(\rho)</math></center>
+La corriente abarcada depende si el radio de la curva de integración es menor o mayor que el del tubo.
+;Interior del tubo: Si <math>\rho < a</math> la circunferencia no abarca ninguna corriente, que fluye completamente por exterior, por lo que
+<center><math>I(\rho) = 0 \qquad (\rho< a)</math></center>
+:y por tanto el campo es nulo en el interior del tubo
+<center><math>\mathbf{B}=\mathbf{0}\qquad (\rho < a)</math></center>
+;Exterior del tubo: Si <math>\rho > a</math> la circunferencia abarca toda la corriente que fluye por el tubo. La corriente que atraviesa un disco apoyado sobre la circunferencia es igual a
+<center><math>I = \int \mathbf{K}\cdot\mathbf{n}_1\mathrm{d}l</math></center>
+:siendo <math>\mathbf{n}_1</math> un vector unitario tangente al cubo y normal al disco. Este vector es <math>\mathbf{u}_z</math>. Por su parte el diferencial de camino sobre esta sección del tubo es
+<center><math>\mathrm{d}l = a\,\mathrm{d}\varphi</math></center>
+:así que queda
+<center><math>I = \int_0^{2\pi}(K\mathbf{u}_z)\cdot\mathbf{u}_z\,a\,\mathrm{d}\varphi = 2\pi A K</math></center>
+:lo que nos da finalmente para el campo magnético en el exterior
+<center><math>\mathbf{B} = \frac{\mu_0aK}{\rho}\mathbf{u}_{\varphi}</math></center>
+Reuniendo ambos resultados
+<center><math>\mathbf{K}=\begin{cases} \mathbf{0} & (\rho < a)\\ & \\ \displaystyle\frac{\mu_0aK}{\rho}\mathbf{u}_{\varphi} & (\rho>a)\end{cases}</math></center>
+Las líneas de campo magnético describen circunferencias en torno al tubo según la regla de la mano derecha. El módulo del campo es nulo en el interior y decae como la inversa de la distancia al eje, esto es, como si toda la corriente estuviera concentrada en el eje del tubo..
 ==En forma diferencial==
+En forma diferencial debemos resolver las ecuaciones de la magnetostática
+<center><math>\begin{array}{rcl}
+\nabla\cdot\mathbf{B} & = & 0 \\ && \\
+\nabla\times\mathbf{B} & = & \mu_0\mathbf{J}=\mathbf{0}
+\end{array}</math></center>
+junto con las correspondientes condiciones de salto en la superficie del cilindro:
+<center><math>\begin{array}{rcl}
+\mathbf{n}\cdot[\mathbf{B}] & = & 0 \\ && \\
+\mathbf{n}\times[\mathbf{B}] & = & \mu_0\mathbf{K}
+\end{array}</math></center>
+Además, debemos tener en cuenta que el campo magnético sólo se puede hacer infinito en puntos donde haya distribuciones de corriente lineales, nunca donde no haya corriente. También que en puntos alejados del cilindro el campo debe anularse.
 Tenemos que, como en el caso del cable grueso, existe simetría traslacional y rotacional. Por ello, ninguna de las tres componentes depende de <math>z</math> ni de <math>\varphi</math>.
@@ Línea 37: / Línea 158: @@
 <center><math>B_\rho=0\,</math></center>
-Del mismo modo, al no haber corrientes de volumen, los campos en el interior y el exterior pueden escribirse como
+Aplicando ahora la ley de Ampère en cada región tenemos
+<center><math>\mathbf{0}=\nabla\times\mathbf{B}=\frac{1}{\rho}\left|\begin{matrix}\mathbf{u}_\rho & \rho\mathbf{u}_\varphi & \mathbf{u}_z \\ & & \\ \displaystyle\frac{\mathrm{d}\ }{\mathrm{d}\rho} & 0 & 0 \\ & & \\ 0 & \rho B_\varphi & B_z\end{matrix}\right| = -\frac{\mathrm{d}B_z}{\mathrm{d}\rho}\mathbf{u}_\varphi + \frac{1}{\rho}\,\frac{\mathrm{d}\ }{\mathrm{d}\rho}(\rho B_\varphi)\mathbf{u}_z</math></center>
+Un vector es nulo cuando son nulas cada una de sus componentes. Por ello, las componentes en el interior y el exterior pueden escribirse como
 <center><math>B_{1z}=a_1\qquad B_{2z}=a_2\qquad B_{1\varphi}=\frac{c_1}{\rho}\qquad B_{2\varphi}=\frac{c_2}{\rho}</math></center>

Campo de un tubo cilíndrico

De Laplace

última version al 22:30 31 may 2011

Contenido

1 Enunciado

2 Introducción

3 En forma integral

4 En forma diferencial

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES